13.5 Feature Structures in Prolog
In this section, we will see how to implement feature structure unification and a subsumption check in Prolog. But first, we have to decide on how to represent feature structures.
13.5.1 Representing Feature Structures in Prolog
We will represent feature structures as a open list of attribute value pairs. An open list is a list with an uninstantiated variable as its tail. [a,b,c|X] is an open list, for instance. So far, it only contains the elements a, b, c, but it can be extended by instantiating the tail, i.e., the variable X, with another (open) list. Instantiating X with [d,e,f|Y], for example, we get [a,b,c,d,e,f|Y].
We will furthermore use : (the colon) to form attribute value pairs: the attribute will be to the left of : and the value to the right. Here is an example of an attribute value pair in Prolog: agr:sg To be able to use the colon in that way we have to declare it as an infix operator:
?-op(500,xfy,:).We will now go through some examples of feature structures and their Prolog representation and make sure that you understand how it works.
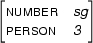
is in Prolog
[number:sg, person:3 | _ ],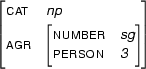
is in Prolog
[cat:np, agr:[number:sg, person:3 | _ ] | _ ],and we will represent
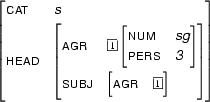
as
[cat:s, head:[agr:[num:sg, pers:3| X ]|_], subj:[agr:[num:sg,pers:3| X ] |_] |_]. Note how we represent the fact that 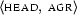 and
and 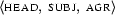 share their value. We duplicate the information that is known about this value, namely that it is a feature structure containing the attribute value pairs
share their value. We duplicate the information that is known about this value, namely that it is a feature structure containing the attribute value pairs 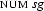 and
and 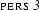 , and we then assign the same variable to the open tail of the two feature structures. This says that these two tails must be the same. So, we have ensured that the values of
, and we then assign the same variable to the open tail of the two feature structures. This says that these two tails must be the same. So, we have ensured that the values of 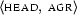 and
and 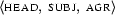 will always be the same. However, this way of representing reentrancy is actually not totally correct. It allows us to write down things which are not valid feature structures, such as
will always be the same. However, this way of representing reentrancy is actually not totally correct. It allows us to write down things which are not valid feature structures, such as
[cat:s, head:[agr:[num:sg, pers:3| X ]|_], subj:[agr:[num:pl,pers:3| X ] |_] |_]. Try to write this feature structure using an attribute value matrix. You will find that you cannot do it, because it is not possible to co-index only parts of feature structures. You would have to say something line "the values of 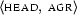 and
and 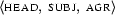 are shared except for the values of of
are shared except for the values of of 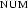 ", but that's not possible to express.
", but that's not possible to express.
13.5.2 Implementing feature structure unification
We shall now implement feature structure unification in Prolog. We do so using an algorithm called destructive unification. Roughly speaking, this algorithm takes as input two feature structure, and then (if it is possible to unify them) builds their unifier. However, it destroys the input feature structures in the process.
For many purposes this is a very good method. For a start, as we shall see, the code is short and (once you understand it) elegant. The code is also efficient, since it essentially works by repeatedly using Prolog unification to combine the parts of the two input feature structures. Finally, when we are doing computational linguistics, often we are only concerned with building the feature structure that corresponds to a sentence. So we don't care if while building this feature structure we destroy the feature structures associated with the subparts.
However, it is important to realize that many different algorithms for performing feature structure unification have been studied --- destructive unification is definitely not the only way of performing feature structure unification! Basically, we are going to discuss destructive unification because it is so simple to implement in Prolog --- but just as there are many ways of performing context-free parsing (top down, bottom up, left corner, passive charts, active chart,...), there are also many ways of implementing feature structure unification. You may encounter some of these other methods in your later studies.
So let's turn to the code. First of all, here's the driver predicate we shall use:
unify(Dag1,Dag2) :-
unify0(Dag1,Dag2),
nl,
write('Result of unification is: '),nl,nl,write(Dag1),
nl. That is, unify/2 takes as input two feature structures written in our Prolog notation, and attempts to unify them by calling a predicate called unify0/2. If unification succeeds, it writes the result.
There's one thing you might find puzzling --- why does it write the value of Dag1 as the result? Isn't Dag1 one of the inputs? Well, yes --- but remember, we are doing destructive unification! That is, at the end of the unification process, the original input values no longer exist: both Dag1 and Dag2 now hold the result of the unification. So the above code is correct. Moreover, we could replace the third line of this driver by:
write('Result of unification is: '),nl, nl, write(Dag2),and this would work just as well (the only difference would be that items in the result might be written in a different order).
So let's get into the real code. What exactly does unify0/2 do, and how is it defined? Here is the complete definition:
unify0(Dag,Dag) :- !.
unify0([Feature:Value|Rest],Dag) :-
val(Feature,Value,Dag,StripDag),
unify0(Rest,StripDag).
val(Feature,Value1,[Feature:Value2|Rest],Rest) :-
!,
unify0(Value1,Value2).
val(Feature,Value,[Dag|Rest],[Dag|NewRest]) :-
!,
val(Feature,Value,Rest,NewRest).Somewhat surprisingly, that is all the Prolog code we need to unify feature structures. How does it work?
The clause
unify0(Dag,Dag) :- !.is the base of the recursion. If we can unify the two open lists representing our feature structures using Prolog unification, we do so and are done. This covers the cases where we get an unistantiated variable in one of the arguments and cases where the open lists are "Prolog unifiable", i.e. order and position of attribute-value pairs matters. For example, if we want to unify the feature structures
[cat:np, num:sg| _]and
[cat:np, num:sg| _] we can just use the Prolog unification to do so. The result will be (of course) [cat:np, num:sg| _]. The same goes for
[cat:np, num:sg| _]and
[cat:np | _]. Here, the result of the unification will be [cat:np, num:sg| _]
The following to cases cannot be unified using just Prolog unification:
[cat:np, num:sg| _]and[num:sg, cat:np| _]: the order in which attributes are listed is not the same.[cat:np | _]and[num:sg | _]: a feature structure can contain attributes that are not mentioned in the other one.
These cases are treated by the recursive clause of unify0/2:
unify0([Feature:Value|Rest],Dag) :-
val(Feature,Value,Dag,StripDag),
unify0(Rest,StripDag). This splits the feature structure in the first argument into the initial pair Feature:Value, and the Rest of the list. Then comes the crucial step: we call val/4 to ensure also in the second feature structure (Dag) the feature Feature has the value Value. Quite a lot happens here --- in fact it is really val/4 which carries out most of the real work. Basically, this is what it does (we'll take a closer look at val shortly):
If
Featureis a feature inDag, and it has a value which is not unifiable withValue, thenval/4will fail; the two feature structures are not unifiable.On the other hand, if
Featureis a feature inDag, and it has a value which is unifiable withValue, thenval/4unifies these two value (via a recursive call tounify0/2).Finally, if
Featureis not a feature inDag, thenval/4adds the pairFeature:ValuetoDag. Here is where the destruction takes place --- we are explicitly adding new information toDag, which is one of the input arguments. ThusDagno longer is the same feature structure we started with.
But that's not all that the call to val/4 does: in its fourth argument it returns a new feature structure, StripDag, which contains everything in Dag apart from the value for Feature. We recursively call unify0/2 on the Rest and StripDag. So, the arguments of the recursive call, Rest and StripDag, are both shorter than the arguments of the original call, [Feature:Value|Rest] and Dag. Hence the recursion is going to terminate.
The point that is worth thinking about here is: why do we only have to unify Rest with StripDag? And the answer should be clear: we've now ensured that the value for Feature is the same in both feature structures. As feature structures are partial functions, there can't be any more information about Feature, so we don't need to carry this information with us any more, and can carry on with StripDag.
We have seen now what unify0/2 does --- but as the above discussion makes clear, most of the work is really being done by val/4. So how does this work?
Here's the first clause. It is really important that you understand it well.
val(Feature,Value1,[Feature:Value2|Rest],Rest) :-
!,
unify0(Value1,Value2). It is really quite simple. If the desired feature, Feature, is the first element fo the list (the feature structure) in the 3rd argument, we check if Value1 can be unified with Value2, via a call to unify0/2 (hence, as should be apparent by now, val/4 and unify0/2 are mutually recursive). Note that the fourth argument is just the tail of the third argument. That is, we've stripped out the first element; or in other words, we have taken the first attribute value pair from the feature structure. One important thing to note here is that this clause will also match, if we get an uninstantiated variable (instead of a list) as third argument. In that case, this variable will be instantiated with an open list that has Feature:Value as its first element.
Now for the the second clause:
val(Feature,Value,[Feature2:Value2|Rest],[Feature2:Value2|NewRest]) :-
!,
val(Feature,Value,Rest,NewRest). This is even simpler. If the desired feature, Feature, is not the first element of the list, we recursively call val/4 on the remainder Rest of the list. If the feature we are looking for is not in the feature structure, we will, at some point, end up with only the (open) tail left. At this point the recursive call of val/4 will be with an uninstantiated variable (the tail) in the third argument. That means that the first clause of val will add the Feature:Value pair to the feature structure.
And that's it. Short and simple. But, it must be admitted, fairly subtle. While no individual part of the above code is complicated, it's probably not easy at first to see how it all fits together. It is a good idea to look at a few examples to get this clear.
First, to understand this code, it is important to get very clear in your mind exactly what it is that val/4 does. We made three remarks about this above. Recall the second of these remarks:
"If Feature is a feature in Dag, and it has a value which is unifiable with Value, then val/4 unifies these two values (via a recursive call to unify0/2)."
For example, consider the following query:
?- val(number,sing,[cat:vp,number:sing|X],Y).
X = _G412
Y = [cat:vp|_G412]
Yes This is exactly what we would expect --- obviously sing unifies with sing. Also, note that we get the `stripped down' version of the third argument returned as the value of the fourth argument.
Here is the (slightly edited) trace of the query to help you understand how val works.
%%% The first call uses the 2nd clause of val:
Call: (1) val(number, sing, [cat:vp, number:sing|X], Y) ?
%%% Now, the 1st clause matches:
Call: (2) val(number, sing, [number:sing|X], Z) ?
%%% obviously sing unifies with itself:
Call: (3) unify(sing, sing) ? s
Exit: (3) unify(sing, sing) ?
%%% So, call 2 is satisfied; X = Z:
Exit: (2) val(number, sing, [number:sing|X], X) ?
%%% And call 1 is satisfied:
Exit: (1) val(number, sing, [cat:vp, number:sing|X], [cat:vp|X]) ? But it is probably the third remark we made above that is most worth emphasizing, namely:
"If Feature is not a feature in Dag, then val/4 adds the pair Feature:Value to Dag."
For example:
?- val(tense,present,[cat:vp,number:sing|X],Y).
X = [tense:present|_G517]
Y = [cat:vp, number:sing|_G517]
yes Prolog let's us know that X, the variable tail of the open list representing the feature structure, has been instantiated with [tense:present|_G517]. Dag is therefore now instantiated with [cat:vp,number:sing,tense:present|_G517]. So, here is where the destruction takes place --- we explicitly added new information (namely, tense:present) to Dag. We no longer have the same feature structure we started with.
Study the following trace of the above query:
%%% 2nd clause of val:
Call: (1) val(tense, present, [cat:vp, number:sing|X], Y) ?
%%% 2nd clause of val:
Call: (2) val(tense, present, [number:sing|X], A) ?
%%% 1st clause of val:
Call: (3) val(tense, present, X, B) ?
Call: (4) unify(present, C) ? s
Exit: (4) unify(present, present) ?
Exit: (3) val(tense, present, [tense:present|B], B) ?
Exit: (2) val(tense, present, [number:sing, tense:present|B], [number:sing|B]) ?
Exit: (1) val(tense, present, [cat:vp, number:sing, tense:present|B], [cat:vp, number:sing|B]) ? So let's look at some examples of the whole program in action. First, a simple example of what happens when unification succeeds:
unify([cat:vp|X],[number:sing|Y]).
Result of unification is:
[cat:vp, number:sing|_G432]
X = [number:sing|_G432]
Y = [cat:vp|_G432]
YesAnd here the trace:
Call: (1) unify([cat:vp|X], [number:sing|Y]) ?
%%% unify calls unify0; 2nd clause of unify0:
Call: (2) unify0([cat:vp|X], [number:sing|Y]) ?
%%% val adds cat:vp to the second feature structure:
Call: (3) val(cat, vp, [number:sing|Y], A) ? s
Exit: (3) val(cat, vp, [number:sing, cat:vp|B], [number:sing|B]) ?
%%% 1st feature structure is empty; 1st clause of unify0:
Call: (3) unify0(X, [number:sing|B]) ?
Exit: (3) unify0([number:sing|B], [number:sing|B]) ?
Exit: (2) unify0([cat:vp, number:sing|B], [number:sing,cat:vp|B]) ?
Exit: (1) unify([cat:vp, number:sing|B], [number:sing, cat:vp|B]) ?Next, a simple example of a unification that fails:
?- unify([cat:vp|Y],[cat:np|X]).
No What happens? The first clause of unify0 doesn't match. Therefore we use the second one. This calls val(cat,vp,[cat:np|X],_). This matches the first clause of val, which fails as vp and np cannot be unified. The cut prohibits backtracking so that the whole query fails.
Here is a slightly more complex example of a unification that succeeds:
?- unify([number:sing,person:third|Y],[case:dative,person:third|X]).
Result of unification is:
[number:sing, person:third, case:dative|_G813]
Y = [case:dative|_G813]
X = [number:sing|_G813]
YesAnd here's a slightly more complex example of a unification that fails:
?- unify([number:sing,person:third|Y],[case:dative,person:second|X]).
NoMake sure that you understand how Prolog arrives at the answers it's giving. Trace through the queries, if necessary.
One final remark. There is one special case of unification that the code given above does not handle properly. Recall that the empty feature structure should unify with anything. Now, in our Prolog notation, the empty feature structure is represented by the empty list, so this means that the query
?- unify([],[agree:[number:sing|Z]|W]).should succeed. But in fact it fails.
Similarly, the query
unify([agree:[number:sing|Z]|W],[])should succeed as well --- but it too fails.
Can you see why this is happening? In fact, this problem is easy to fix by modifying the driver predicate unify/2 so that it looks out for these special cases and handles them appropriately. You are asked to do this as a practical exercise.
13.5.3 Subsumption in Prolog
Finally, we will implement a predicate that checks whether one feature structure subsumes another feature structure. The implementation will make use of the predicate unify0/2.
If feature structure 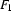 subsumes feature structure
subsumes feature structure 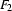 , then there is no information in
, then there is no information in 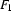 which is not in
which is not in 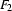 . That means we can unify
. That means we can unify 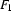 and
and 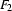 without further instantiating
without further instantiating 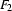 , i.e.
, i.e. 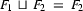 . So, one strategy for checking subsumption would be to unify
. So, one strategy for checking subsumption would be to unify 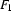 and
and 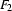 and afterwards check whether the result is exactly
and afterwards check whether the result is exactly 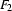 . Here, we will use the following strategy: We make sure that it is impossible to add information to
. Here, we will use the following strategy: We make sure that it is impossible to add information to 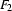 . Then we try to unify. If that's possible, then
. Then we try to unify. If that's possible, then 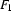 subsumes
subsumes 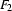 . If it's not possible, then
. If it's not possible, then 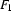 doesn't subsume
doesn't subsume 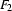 .
.
But how are we going to make sure that no new information can be added to 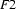 ? The way our implementation of feature structures works adding information means instantiating variables. So, we have to make sure that variables cannot be instantiated during unification. The easiest way to do this is to (temporarily) instantiate them with some atom. And this is what we are going to do: we are going to instantiate all variables in the Prolog representation of
? The way our implementation of feature structures works adding information means instantiating variables. So, we have to make sure that variables cannot be instantiated during unification. The easiest way to do this is to (temporarily) instantiate them with some atom. And this is what we are going to do: we are going to instantiate all variables in the Prolog representation of 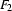 with atoms. To keep track of reentrancy, we will instantiate different variables with different atoms.
with atoms. To keep track of reentrancy, we will instantiate different variables with different atoms.
Here is the predicate inst_vars which instantiates all variables in a Prolog representation of a feature structure with atoms of the form v(0), v(v(0)), v(v(v(0))) and so on.
inst_vars(F) :-
inst_vars0(F,v(0),_).
inst_vars0(F,I,v(I)) :-
var(F),!,
F = I.
inst_vars0([],I,I) :- !.
inst_vars0([H|T],I,IOut) :- !,
inst_vars0(H,I,I0),
inst_vars0(T,I0,IOut).
inst_vars0(_F:V,I,IOut) :- !,
inst_vars0(V,I,IOut).
inst_vars0(_,I,I). Now, that we have this predicate, we just have to use it, to instantiate all variables in 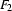 and then we can use the predicate
and then we can use the predicate unify0 to check whether (the instantiated) 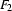 and
and 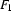 unify.
unify.
subsumes(F1,F2) :-
inst_vars(F2),
unify0(F1,F2).Here are some examples of how it works:
?- subsumes([cat:np|X],[cat:np,num:sg|Y]).
X = [num:sg|v(0)]
Y = v(0)
Yes
?- subsumes([cat:np,num:sg|Y],[cat:np|X]).
No Correctly, Prolog answers Yes in the first case and fails in the second. But, there is still a problem with this definition of subsumes. Maybe you have already spotted it. In the first case, we not only check for subsumption, but also destructively unify the feature structures. And in addition, all variables, like the open tails, are instantiated. Of course, that's how we defined subsumes (using inst_vars and unify0), but it would be nice, if we could get rid of the instantiations again in the end. To this end, we will use the fact that instantiations done within the scope of a negation don't get out of there. So, instead of saying "subsumes suceeds if we can instantiate all variables of 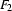 and unify", we will say "it succeeds if it is not the case that after instantiating all variables of
and unify", we will say "it succeeds if it is not the case that after instantiating all variables of 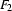 it is not possible to unify
it is not possible to unify 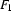 and
and 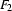 . Here is the code:
. Here is the code:
subsumes(F1,F2) :-
\+ (inst_vars(F2),
\+ (unify0(F1,F2))).