13.4 Feature Structure Unification
Unification is a (partial) operation on feature structures. Intuitively, it is the operation of combining two feature structures such that the new feature structure contains all the information of the original two, and nothing more. For example, let 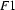 be the feature structure
be the feature structure
and let 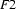 be the feature structure
be the feature structure
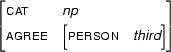
Then, 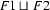 , the unification of these two feature structures is:
, the unification of these two feature structures is:
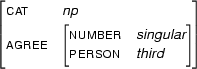
Clearly 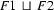 contains all the information that is in
contains all the information that is in 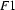 and
and 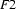 --- and it doesn't contain any other information.
--- and it doesn't contain any other information.
Why did we call unification a partial operation? Why didn't we just say that it was an operation on feature structures? The point is that unification is not guaranteed to return a result. For example, let 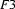 be the feature structure
be the feature structure
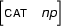
and let 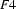 be the feature structure
be the feature structure
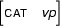
Then 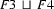 does not exist. There is no feature structure that contains all the information in
does not exist. There is no feature structure that contains all the information in 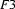 and
and 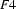 , because the information in these two feature structures is contradictory. So, the value of this unification is undefined.
, because the information in these two feature structures is contradictory. So, the value of this unification is undefined.
Those are the basic intuitions about unification, so let's now give a precise definition. This is easy to do if we make use of the idea of subsumption, which we discussed above.
The unification of two feature structures  and
and 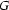 (if it exists) is the smallest feature structure that is subsumed by both
(if it exists) is the smallest feature structure that is subsumed by both  and
and 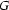 . That is,
. That is, 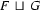 (if it exists) is the feature structure with the following three properties:
(if it exists) is the feature structure with the following three properties:
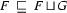 (
(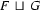 is subsumed by
is subsumed by  )
)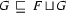 (
(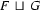 is subsumed by
is subsumed by 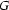 )
)If
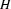 is a feature structure such that
is a feature structure such that 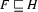 and
and 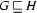 , then
, then 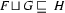 (
(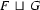 is the smallest feature structure fulfilling the first two properties. That is, there is other feature structure that also has properties 1 and 2 and subsumes
is the smallest feature structure fulfilling the first two properties. That is, there is other feature structure that also has properties 1 and 2 and subsumes 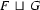 .)
.)
If there is no smallest feature structure that is subsumed by both  and
and 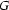 , then we say that the unification of
, then we say that the unification of  and
and 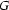 is undefined.
is undefined.
We said above that the subsumption relation  on feature structures can be thought of as analogous to the subset relation on sets. Similarly, unification
on feature structures can be thought of as analogous to the subset relation on sets. Similarly, unification  is rather like an analog of set-theoretic union (recall that the union of two sets is the smallest set that contains all the elements in both sets). But there is a difference: union of sets is an operation (that is, the union of two sets is always defined) whereas (as we have discussed) unification is only a partial operation on feature structures.
is rather like an analog of set-theoretic union (recall that the union of two sets is the smallest set that contains all the elements in both sets). But there is a difference: union of sets is an operation (that is, the union of two sets is always defined) whereas (as we have discussed) unification is only a partial operation on feature structures.
Now that the formal definition is in place, let's look at a few more examples of feature structure unification. First, let 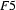 be
be
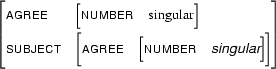
and let 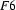 be the feature structure
be the feature structure
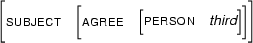
Then 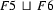 is
is
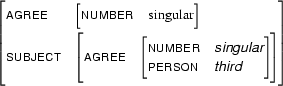
Next, an example involving reentrancies. Let 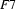 be
be
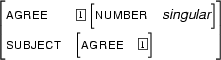
Then  is
is
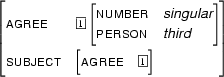
A final example. What happens if one of the feature structures we are trying to unify is the empty feature structure ![[ \ ]](latex302.gif) --- that is, the feature structure containing no information at all? Pretty clearly, for any feature structure
--- that is, the feature structure containing no information at all? Pretty clearly, for any feature structure  , we have that:
, we have that:
That is, the empty feature structure is the identity element for the (partial) operation on feature structure unification. That is, the empty feature structure behaves like the empty set in set theory (recall that the union of the empty set with any set 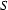 is just
is just  ).
).
That concludes our discussion of feature structure unification --- but before going on to discuss how to implement it in Prolog, let's briefly look at an operation of feature structures called generalization.
Generalization can be thought of as an analog of the set-theoretic operation of intersection. Recall that the intersection of two sets is the set that contains only the elements common to both sets. Similarly, the generalization of two feature structures contains only the information that is common to both feature structures.
For example, let 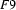 be
be
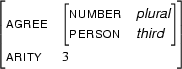
and let  be
be
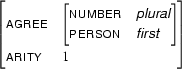
Then 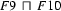 , the generalization of
, the generalization of 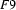 and
and 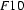 , is
, is
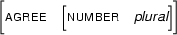
Clearly 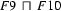 contains only information which can be found in both
contains only information which can be found in both 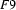 and
and 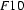 .
.
Here's a precise definition of generalization: The generalization of two feature structures  and
and 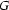 is the largest feature structure that subsumes both
is the largest feature structure that subsumes both  and
and 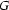 . That is,
. That is, 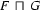 is the feature structure with the following three properties:
is the feature structure with the following three properties:
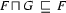
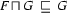
If
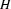 is a feature structure such that
is a feature structure such that 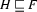 and
and 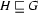 , then
, then 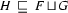
There is an important difference between unification and generalization: unlike unification, generalization is an operation on feature structures, not just a partial operation. That is, the generalization of two features is always defined. Think about it. Consider the worst case --- two feature structures  and
and 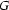 that contain no common information at all. Is there a largest feature structure that subsumes both? Of course there is --- the empty feature structure
that contain no common information at all. Is there a largest feature structure that subsumes both? Of course there is --- the empty feature structure ![[ \ ]](latex302.gif) !
!
Thus, from a mathematical perspective, generalization is somewhat easier to work with than unification. Nonetheless, it is not used nearly so often in computational linguistics as unification is, so we won't discuss how to implement it. But implementing generalization in Prolog is a very interesting task; one you may like to try for yourself.
![F \sqcup \ [ \ ] = [ \ ] \ \sqcup
\ F = F](latex303.gif)