7.3 Putting it in Prolog

The main goal of this section is to write a simple bottom up recognizer in Prolog. But before we do this, we have to decide how to represent CFGs in Prolog. The representation that we are going to introduce distinguished between phrase structure rules and lexical rules by representing them in different ways. As we mentioned above, it is often useful to be able to make this distinction when dealing with natural languages. For representing phrase structure rules, we shall use a notation that is quite close to the one used in DCGs. In fact, there are only two differences. First, whereas DCGs use the symbol

-->

for the rewrite arrow, we shall use the symbol

--->

Second, in DCGs we would write 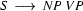$S\ \longrightarrow\ NP\ VP$ as:

s --> np,vp.

However we shall use instead the following notation:

s ---> [np,vp].

Here's an example. The phrase structure rules of our earlier English grammar become in this notation :

s ---> [np,vp]. np ---> [pn]. np ---> [pn,rel]. np ---> [det, nbar]. nbar ---> [n]. nbar ---> [n,rel]. rel ---> [wh,vp]. vp ---> [iv]. vp ---> [tv,np]. vp ---> [dv,np,pp]. vp ---> [sv,s]. pp ---> [p,np].

How does Prolog know about the symbol --->? Well, it needs to be told what it means, and we can do this using an operator definition as follows:

?- op(255,xfx,--->).

That is, we have declared ---> to be a binary infix operator. The best place to put this definition is probably in the recognizer, not in each and every grammar. But note: this means you will have to consult the recognizer before you consult any of the the grammars, as otherwise Prolog won't know what ---> means.

Now, we can represent phrase structure rules. Lexical rules we shall represent using the predicate lex/2. For example, 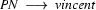$PN\ \longrightarrow\ vincent$ will be represented as lex(vincent,pn). Here are the lexical rules of the little English grammar that we have seen above in the new notation.

lex(vincent,pn). lex(mia,pn). lex(marsellus,pn). lex(jules,pn). lex(a,det). lex(the,det). lex(her,det). lex(his,det). lex(gun,n). lex(robber,n). lex(man,n). lex(woman,n). lex(who,wh). lex(that,wh). lex(to,p). lex(died,iv). lex(fell,iv). lex(loved,tv). lex(shot,tv). lex(knew,tv). lex(gave,dv). lex(handed,dv). lex(knew,sv). lex(believed,sv).

Incidentally --- we shall use this notation for grammars throughout the course. All our parser/recognizers will make us of grammars in this format.

It's now time to define our very first recognizer --- a simple (though inefficient) recognizer which carries out the algorithm sketched above. Here it is. The predicate recognize_bottomup/1 takes as input a list of symbols (for example, [vincent,shot,marsellus]) and tries to build the list [s] (that is, a sentence). Here is its definition:

recognize_bottomup([s]). recognize_bottomup(String) :- split(String,Front,Middle,Back), ( Cat ---> Middle ; (Middle = [Word], lex(Word,Cat)) ), append(Front,[Cat|Back],NewString), recognize_bottomup(NewString).

How does this work? Well, the first clause, recognize_bottomup([s]), tells us that we have succeeded if we find the list [s]. Incidentally, if you glance down at the following clause, you will see that recognize_bottomup/1 is recursive. This first clause is the base clause of the recursion.

So what about the second clause? First we have:

split(String,Front,Middle,Back)

The predicate split/4 splits a list into three parts. It is defined as follows:

split(ABC, A, B, C) :- append(A, BC, ABC), append(B, C, BC).

split/4 uses the standard append/3 predicate to split up the incoming list by calling it with uninstantiated varibles in the first two arguments. append/3 is called twice: The first time the incoming list is split in two parts, and the second time one of the parts is again split into two parts, resulting in three parts altogether. Unfortunately, using append/3 in this way is very inefficient.

So --- split/4 splits the string into three parts: Front, Middle, and Back. Next comes a disjunction:

Cat ---> Middle ; (Middle = [Word], lex(Word,Cat))

It succeeds if we have either a phrase structure rule with Middle as its right hand side, or if Middle is actually a word that we can map to a category by a lexical rule.

Now for the key step. Suppose we have such a rule. Then

append(Front,[Cat|Back],NewString)

builds a new string by replacing Middle with Cat. That is, from

Front Middle Rest

we get the new string

Front Cat Rest

In short: we have used our rule right to left to build a new string.

The rest is simple. We recursively call

recognize_bottomup(NewString),

on the new string we have built. If we have a sentence on our hands, this recursion will eventually produce [s], and we will succeed using the first clause. Note that every call to recognize_bottomup/1 makes use of append/3 to decompose the input list. So, via backtracking, we will eventually find all possible ways of decomposing the input list --- thus if the input really is a sentence, we will eventually succeed in showing this.

Let's look at an example, to see if we've got it right. If you ask Prolog

recognize_bottomup([vincent,shot,marsellus])

, it will answer yes, as it should. Try some other examples and check whether Prolog answers the way it should. A trace will give you more information about how Prolog is arriving at these answers. Here is an abbreviated trace for the query recognize_bottomup([vincent,shot,marsellus]). You can see how Prolog splits up the string that is to be recognized into three parts, which rules it applies for replacing the middle part with a category symbol, and you can see the recursive calls of recognize_bottomup that it makes.

?- recognize_bottomup([vincent,shot,marsellus]). Call: (7) recognize_bottomup([vincent, shot, marsellus]) ? Call: (8) split([vincent, shot, marsellus], _G647, _G648, _G649) ? Exit: (8) split([vincent, shot, marsellus], [], [vincent], [shot, marsellus]) ? Call: (8) lex(vincent, _G653) ? Exit: (8) lex(vincent, pn) ? Call: (8) recognize_bottomup([pn, shot, marsellus]) ? Call: (9) split([pn, shot, marsellus], _G656, _G657, _G658) ? Exit: (9) split([pn, shot, marsellus], [], [pn], [shot, marsellus]) ? Call: (9) _G658--->[pn] ? Exit: (9) np--->[pn] ? Call: (9) recognize_bottomup([np, shot, marsellus]) ? Call: (10) split([np, shot, marsellus], _G662, _G663, _G664) ? Exit: (10) split([np, shot, marsellus], [np], [shot], [marsellus]) ? Call: (10) lex(shot, _G671) ? Exit: (10) lex(shot, tv) ? Call: (10) recognize_bottomup([np, tv, marsellus]) ? Call: (11) split([np, tv, marsellus], _G677, _G678, _G679) ? Exit: (11) split([np, tv, marsellus], [np, tv], [marsellus], []) ? Call: (11) lex(marsellus, _G689) ? Exit: (11) lex(marsellus, pn) ? Call: (11) recognize_bottomup([np, tv, pn]) ? Call: (12) split([np, tv, pn], _G698, _G699, _G700) ? Exit: (12) split([np, tv, pn], [np, tv], [pn], []) ? Call: (12) _G706--->[pn] ? Exit: (12) np--->[pn] ? Call: (12) recognize_bottomup([np, tv, np]) ? Call: (13) split([np, tv, np], _G716, _G717, _G718) ? Exit: (13) split([np, tv, np], [np], [tv, np], []) ? Call: (13) _G724--->[tv, np] ? Exit: (13) vp--->[tv, np] ? Call: (13) recognize_bottomup([np, vp]) ? Call: (14) split([np, vp], _G731, _G732, _G733) ? Exit: (14) split([np, vp], [], [np, vp], []) ? Call: (14) _G736--->[np, vp] ? Exit: (14) s--->[np, vp] ? Call: (14) recognize_bottomup([s]) ? Exit: (14) recognize_bottomup([s]) ? Exit: (13) recognize_bottomup([np, vp]) ? Exit: (12) recognize_bottomup([np, tv, np]) ? Exit: (11) recognize_bottomup([np, tv, pn]) ? Exit: (10) recognize_bottomup([np, tv, marsellus]) ? Exit: (9) recognize_bottomup([np, shot, marsellus]) ? Exit: (8) recognize_bottomup([pn, shot, marsellus]) ? Exit: (7) recognize_bottomup([vincent, shot, marsellus]) ? Yes

This trace only shows the essence of how the recognizer arrives at its answer. I cut out all the rest. Try it yourself and you will see that the recognizer spends a LOT of time trying out different ways of splitting up the string.