4.3 Theoretical Remarks

The ability to use named subnetworks is certainly a great practical advantage of RTNs over FSAs --- it makes it much easier for us to organize linguistic data. But it should be clear that the really interesting new idea in RTNs is not just the use of subnetworks, but the {\em recursive/ use of such subnetworks. And now for two important questions. Does the ability to use subnetworks recursively really give us additional power to recognizes/generate languages? And if so, how much power does it give us?

Let's answer the first question. Yes, the ability to use subnetworks recursively really {\em does/ offer us extra power. Here's a simple way to see this. As I remarked in an earlier lecture, it is {\em impossible/ to write an FSA that recognizes/generates the formal language 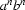a^nb^n . Recall that this is the formal language consisting of precisely those strings which consist of a block of as followed by a block of bs. That is, the number of as and bs must be exactly the same (note that the empty string, $\epsilon$ , belongs to this language).

However, it is very easy to write a RTN that recognizes/generates this language. Here's how:

--------------------------------------- s | | -- | # | -> 1 ----------------> 4 -> | | | | | | | a \/ /\ b | | | | | | | 2 ----------------> 3 | s | | ---------------------------------------

This RTN consists of a single subnetwork (named s) that recursively calls itself.

Let's check that this really works by looking at what happens when we recognize aaabbb. (In this example I won't bother writing states as ordered pairs --- as there is only one subnetwork, each node is uniquely numbered.)

Tape and Pointer State Stack Comment Step 1: aaabbb 1 empty ^ Step 2: aaabbb 2 empty ^ Step 3: aaabbb 1 3 Push ^ Step 4: aaabbb 2 3 ^ Step 5: aaabbb 1 3,3 Push ^ Step 6: aaabbb 2 3,3 ^ Step 7: aaabbb 1 3,3,3 Push ^ Step 8: aaabbb 4 3,3,3 ^ Step 9: aaabbb 3 3,3 Pop ^ Step 10: aaabbb 4 3,3 ^ Step 11: aaabbb 3 3 Pop ^ Step 12: aaabbb 4 3 ^ Step 13: aaabbb 3 empty Pop ^ Step 14: aaabbb 4 empty ^

So, after 14 steps, we have read all the symbols (the pointer is immediately to the right of the last symbol), we are in a final state (namely 4), and the stack is empty. So this RTN really does recognize aaabbb. And from this example it should be pretty clear that this RTN can recognize/generate the language 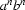a^nb^n . So RTNs can do things that FSAs cannot.

This brings us to the second question. We now know that RTNs can do more than FSAs can --- but how much more can they do? Exactly which languages can be recognized/generated by RTNs?

There is an elegant answer to this question: RTNs can recognize/generate precisely the context free languages. That is, if a language is context free, you can write an RTN that recognizes/generates it; and, conversely, if you can write an RTN that recognizes/generates some language, then that language is context free.

Now, we haven't yet discussed context-free languages in this course (we will spend a lot of time on them later on) but we discussed them a little in the first Prolog, course and you have certainly come across this concept before. Basically, a context free grammar is written using rules like the following:

S $\longrightarrow$ NP VP

NP $\longrightarrow$ Det N

Note that there is only over one symbol to the left hand side of the 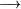$\longrightarrow$ symbol; this is the restriction that makes a grammar `context free'. And a language is context free if there is some context free grammar that generates it.

There is a fairly clear connection between context free grammars and RTNs. First, it is easy to turn a context free grammar into an RTN. For example, consider the following context free grammar:

S $\longrightarrow$ $\epsilon$

S $\longrightarrow$ a S b

Rule 1 says that an can be rewritten as nothing at all (the $\epsilon$ stands for the empty string). Rule 2 says that an 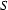can be rewritten as an a followed by an 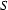followed by a b. Note that this second rule is recursive --- the definition of how to rewrite 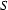makes use of .

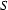If you think about it, you will see that this little context free grammar generates the language 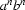a^nb^n discussed above. For example, we can rewrite 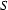to aaabbb as follows:

S	rewrite using Rule 2
aSb	rewrite using Rule 2
aaSbb	rewrite using Rule 2
aaaSbbb	rewrite using Rule 1
aaabbb

And if you think about it a little more, you will see that this context free grammar directly corresponds to the RTN we drew above:

The 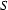corresponds to the name of the subnetwork (that is, s).
Each rule corresponds to a path through the S subnetwork from an initial to a final node. The first rule (the $\epsilon$ rule) corresponds to the jump arc, and the second rule (the recursive rule) corresponds to the recursive transition through the network (that is, the transition where the s subnetwork recursively calls itself)

OK --- I haven't spelt out all the details, but the basic point should be clear: given a context free grammar, you can turn it into an RTN.

But you can also do the reverse: given an RTN, you can turn it into a context free grammar. For example, consider the following context free grammar:

S $\longrightarrow$ NP VP

NP $\longrightarrow$ Det N

V $\longrightarrow$ NP VP

N $\longrightarrow$ wizard

N $\longrightarrow$ broomstick

NP $\longrightarrow$ Harry

NP $\longrightarrow$ Voldemort

Det $\longrightarrow$ a

Det $\longrightarrow$ the

V $\longrightarrow$ flies

V $\longrightarrow$ curses

This context free grammar corresponds in a very straightforward way to our very first RTN. The symbols on the left hand side are either subnetwork names or category symbols, and the right hand side is either a path through a subnetwork, or a word that belongs to the appropriate category.