4.2 A Closer Look

How exactly do RTNs work? In particular, what information do we have to keep track of when using an RTN in recognition mode?

Now, the first two parts of the answer are clear from our earlier work on FSAs. If we want to recognize a string with an RTN, it is pretty clear that we are going to have to keep track of (1) which symbol we are reading on the input tape, and (2) which state the RTN is in. OK --- things are slightly more complicated for RTNs as regards point (2). For example, it's not enough to remember that the machine is in state 0, as several subnetworks may have a state called 0. But this is easy to arrange. 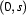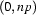For example, ordered pairs such as (0,s) or (0,np) uniquely identify which state we are interested in, so we simply need to keep track of such pairs. But this (small) complication aside, things are pretty much the same as with FSAs --- at least, so far.

But there is something else vital we need to keep track of:

which state we return to after we have traversed another subnetwork.

This is something completely new --- what do we do here?

This question brings us to one of the key ideas underlying the use of RTNs: the use of stacks. Stacks are one of the most fundamental data structures in computer science. In essence they are a very simple way of storing and retrieving information, and RTNs make crucial use of stacks. So: what exactly is a stack?

4.2.1 Stacks

A stack can be though of as an ordered list of information. For example

a 23 4 foo blib gub 2

is a stack containing seven items. But what makes a stack a stack is that items can only be added or removed from a stack from one particular end. This `active end' --- the one where data can be added or removed --- is called the top of the stack. We shall represent stacks as horizontal lists like the one just given, and when we do this, the left most position represents the top of the stack. Thus, in our previous example, `a' is the topmost item on the stack.

As I said, all data manipulation takes place via top. Moreover, there are only two data manipulation operations: push and pop.

The push operation adds a new piece of data to the top of a stack. For example, if we push 5 onto the previous stack we get

5 a 23 4 foo blib gub 2

The pop operation, on the other hand, removes the top item from the stack. For example, performing pop on the previous stack removes the top item from the stack, thus giving us the value 5, and stack is now like it was before:

a 23 4 foo blib gub 2

If we perform three more pops we get the value 4, and the following stack is left behind

foo blib gub 2

Thus, stacks work on a `last in, first out' principle. The last thing to be added to a stack (via push) is the first item that can be removed (via pop).

There is a special stack, the empty stack, which we write as follows

empty

We are free to push new values onto an empty stack. For example, if we push 2 onto the empty stack we obtain the stack

2

On the other hand, we cannot pop anything off the empty stack --- after all, there's nothing to pop. If we try to pop the empty stack, we get an error.

4.2.2 Stacks and RTNs

Stacks are used to control the calling of subnetworks in RTNs. In particular:

Suppose we are in a network 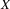, and suppose that traversing the subnetwork would take us to state 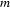in subnetwork 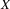. Then we push the state/subnetwork pair 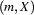onto the stack and try to make the traversal.
That is, the stack tells us where to return to if the traversal is successful.
For example, in RTN1, if we were in the vp network at node 1, we could get to node 2 by traversing the np subnetwork. So, before we try to make the traversal we push (2,vp) onto the stack. If the traversal is successful, we return to state 2 in subnetwork vp at the end of it.
But how, and when, do we return? With the help of pop. Suppose we have just successfully traversed subnetwork . That is, we have reached a final state for subnetwork . Do we halt? Not necessarily --- we first look at the stack:
- If the stack is empty, we halt.
- If the stack is not empty, we jump the the state/subnetwork pair recorded on the stack.
Because stacks work on the `last in, first out' principle, popping the stack always takes us back to the relevant state/subnetwork pair.

That's the basic idea --- and we'll shortly give an example to illustrate it. But before we do this, let's define what it means to recognize a string. A subnetwork of an RTN recognizes a string, if when when we start with the RTN in an initial state of that subnetwork, with the pointer pointing at the first symbol on the input tape, and with an empty stack, we can carry out a sequence of transitions and end up as follows:

In a final state of the subnetwork we started in,
with the pointer pointing to the square immediately after the last symbol of the input, and
with an empty stack.

Incidentally, in theoretical computer science, RTNs are usually called pushdown automata, and it should now be clear why.

4.2.3 An Example

Let's see how all this works. Consider the sentence Harry flies a broomstick. Intuitively, this should be accepted by RTN1 (and indeed, RTN2) but let's go through the example carefully to see exactly how this comes about.

So: we want to to show that Harry flies a broomstick is a sentence. So we have to start off (a) in an initial state of the s network, (b) with the pointer scanning the first symbol of the input (that is, `Harry')

Tape and Pointer State Stack Comment Step 1: Harry flies a broomstick (0,s) empty ^ Step 2: Harry flies a broomstick (1,s) empty ^ Step 3: Harry flies a broomstick (0,vp) (2,s) Push ^ Step 4: Harry flies a broomstick (1,vp) (2,s) ^ Step 5: Harry flies a broomstick (0,np) (2,vp) (2,s) Push ^ Step 6: Harry flies a broomstick (1,np) (2,vp) (2,s) ^ Step 7: Harry flies a broomstick (2,np) (2,vp) (2,s) ^ Step 8: Harry flies a broomstick (2,vp) (2,s) Pop ^ Step 9: Harry flies a broomstick (2,s) empty Pop ^

So: have we recognized the sentence? Yes: at Step 9 we are (a) in a final state of subnetwork s (namely state 2), (b) scanning the tape immediately to the right of the last input symbol, and (c) we have an empty stack.

This example illustrates the basic way stacks are used to control RTNs. We shall see another example, involving recursion, shortly.