1.2 Some Examples

Now, let's have a look at some more examples of what finite state automata can look like.

Assume that we want to extend our laughing machine so that it not only recognizes sequences of ha (followed by !) as laughter but also sequences of ho (followed by !) and sequences mixing has and hos (followed by !). So, as may now be replaced by os. This means that in all states where the machine can make an a transition, it should now also be able to make an o transition. So, all we have to do to extend our machine in this way is to add an o transition from state 2 to state 3.

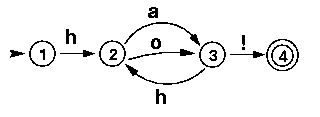
Now, look at the following FSA:

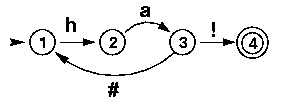
It has a strange transition from state 3 to state 1 which is reading/emitting #. We will call transitions of this type jump arcs. Jump arcs let us jump from one state to another without emitting or reading a symbol. So, # is really just there to indicate that this is a jump arc and the machine is not reading or writing anything when making this transition. This FSA accepts/generates the same language as our first laughing machine, namely sequences of ha followed by a !.

And what language does this FSA accept/generate?

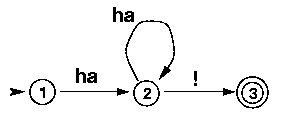
It also accepts/generates the same language as our first laughing machine. But the alphabet it uses is a bit different. Here ha counts as one symbol and can therefore be read by one transition. Furthermore, the FSA has a reflexive transition, going from state 2 back to itself.

Finally, an FSA can have several intial and final states (it must have at least one initial and one final state, though). Here is a machine that has two final states. What language does it recognize?

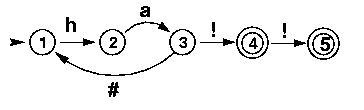
The machine can stop after having generated one exclamation mark or after having generated two exclamation mark. So, the words of the language it accepts/generates all consist of a sequence of ha followed by either one ! or two !.