1.1 Finite State Recognizers and Generators

Finite state automata are used a lot for all kinds of things in computational linguistics. For example, they are used in morphology, phonology, text to speech, data mining ... Why are they so popular? Well, they are very simple (as you will see for yourself, soon) and extremely well understood mathematically. Furthermore, they are easy to implement (this, you will also see soon) and usually these implementations are very efficient. Therefore, finite state solutions tend to be good solutions. However, something so simple and efficient, has to be restricted in what it is able to do in some way, which means that there isn't a finite state solution for every problem. We will look at some limitations of finite state methods later in this chapter. But first, let's see what finite state automata are and what they can do.

1.1.1 A Simple Machine that can laugh

A finite state generator is a simple computing machine that outputs a sequence of symbols.

It starts in some start state

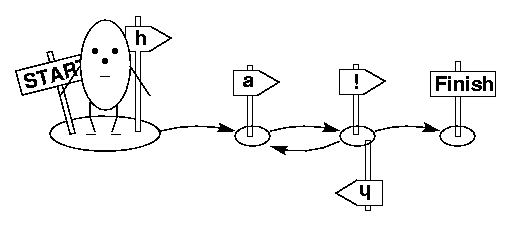
and then tries to reach a final state by making transitions from one state to another. Every time it makes such a transition it emits (or writes or generates) a symbol.

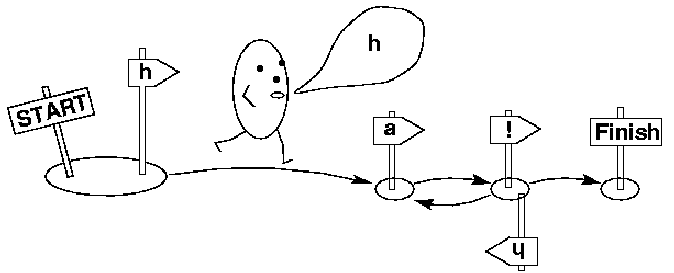
It has to keep doing this until it reaches a final state; before that it cannot stop. All in all, finite state generators can only have a finite number of different states, that's where the name comes from. Another important property of finite state generators is that they only know the state they are currently in. That means they cannot look ahead at the states that come and also don't have any memory of the states they have been in before or the symbols that they have emitted.

So, what does the generator in the pictures say? It laughs. It generates sequences of symbols of the form ha! or haha! or hahaha! or hahahaha! and so on. Why does it behave like that? Well, it first has to make a transition emitting h. The state that it reaches through this transition is not a final state. So, it has to keep on going emitting an a. Here, it has two possibilities: it can either follow the ! arrow, emitting ! and then stopping in the final state (but remember, it can't look ahead to see that it would reach a final state with the ! transition) or it can follow the h arrow emitting an h and going back to the state where it just came from.

Finite state generators can be thought of as directed graphs. And in fact finite state generators are usually drawn as directed graphs. Here is our laughing machine as we will from now on draw finite state generators:

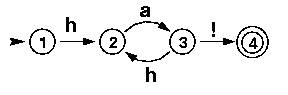
The nodes of the graph are the states of the generator. We have numbered them, so that it is easier to talk about them. The arcs of the graph are the transitions, and the labels of the arcs are the symbols that the machine emits. A double circle indicates that this state is a final state and

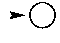
is a start state.

1.1.2 Finite State Automata

In the previous section, we have learned that finite state generators are simple computing machines that output a sequence of symbols. Finite state recognizers are simple computing machines that read (or at least try to read) a sequence of symbols from an input tape. That seems to be only a small differnce, and in fact, finite state generators and finite state recognizers are exactly the same kind of machine. Just that we are using them to output symbols in one case and to read symbols in the other case. The general term for such machines is finite state automaton (FSA) or finite state machine (FSM). But let's have a closer look at what it means for a finite state automaton to recognize a string of symbols.

An FSA recognizes (or accepts) a string of symbols (or word) 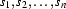$s_1, s_2, \ldots ,s_{n}$ if starting in an intial state it can read in the symbols one after the other while making transitions from one state to another such that the transition reading in the last symbol takes the machine into a final state. That means an FSA fails to recognize a string if:

it cannot reach a final state; or
it can reach a final state, but when it does there are still unread symbols left over

So, this machine

recognizes laughter. For example, it accepts the word ha! by going from state 1 via state 2 and state 3 to state 4. At that point it has read all of the input and is in a final state. It also accepts the word haha! by making the following sequence of transitions: state 1, state 2, state 3, state 2, state 3, state 4. Similarly, it accepts hahaha! and hahahaha! and so on. However, does it accept the word haha? No! Although it will be able to read the whole input (state 1, state 2, state 3, state 2, state 3), it will end in a non-final state without anything left to read that could take it into the final state. Does it accept hoho!? No, because with this input, it won't be able to read the whole input (there is no transition that allows reading an o.

So, when used in recognition mode, this machine recognizes exactly the same words that it generates, when used in generation mode. This is something which is true for all finite state automata and we can make it more precise:

A formal language is a set of strings.
The language accepted (or recognized) by an FSM is the set of all strings it recognizes when used in recognition mode.
The language generated by an FSM is the set of all strings it can generate when used in generation mode.
The language accepted and the language generated by an FSM are exactly the same.