10.1 The cut

Automatic backtracking is one of the most characteristic features of Prolog. But backtracking can lead to inefficiency. Sometimes Prolog can waste time exploring possibilities that lead nowhere. It would be pleasant to have some control over this aspect of its behaviour, but so far we have only seen two (rather crude) ways of doing this: changing the order of rules, and changing the order of conjuncts in the body of rules. But there is another way. There is an inbuilt Prolog predicate !, called cut, which offers a more direct way of exercising control over the way Prolog looks for solutions.

What exactly is cut, and what does it do? It's simply a special atom that we can use when writing clauses. For example,

p(X) :- b(X),c(X),!,d(X),e(X).

is a perfectly good Prolog rule. As for what cut does, first of all, it is a goal that always succeeds. Second, and more importantly, it has a side effect. Suppose that some goal makes use of this clause (we call this goal the parent goal). Then the cut commits Prolog to any choices that were made since the parent goal was unified with the left hand side of the rule (including, importantly, the choice of using that particular clause). Let's look at an example to see what this means.

Let's first consider the following piece of cut-free code:

p(X) :- a(X). p(X) :- b(X),c(X),d(X),e(X). p(X) :- f(X). a(1). b(1). c(1). b(2). c(2). d(2). e(2). f(3).

If we pose the query p(X) we will get the following responses:

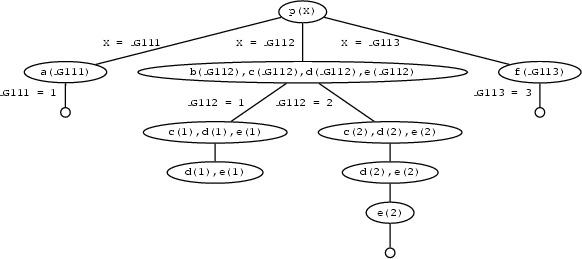
X = 1 ; X = 2 ; X = 3 ; no

Here is the search tree that explains how Prolog finds these three solutions. Note, that it has to backtrack once, namely when it enteres the second clause for p/1 and decides to match the first goal with b(1) instead of b(2).

But now supppose we insert a cut in the second clause:

p(X) :- b(X),c(X),!,d(X),e(X).

If we now pose the query p(X) we will get the following responses:

X = 1 ; no

What's going on here? Lets consider.

p(X) is first matched with the first rule, so we get a new goal a(X). By instantiating X to 1, Prolog matches a(X) with the fact a(1) and we have found a solution. So far, this is exactly what happened in the first version of the program.
We then go on and look for a second solution. p(X) is matched with the second rule, so we get the new goals b(X),c(X),!,d(X),e(X). By instantiating X to 1, Prolog matches b(X) with the fact b(1), so we now have the goals c(1),!,d(1),e(1). But c(1) is in the database so this simplifies to !,d(1),e(1).
Now for the big change. The ! goal succeeds (as it always does) and commits us to all the choices we have made so far. In particular, we are committed to having X = 1, and we are also committed to using the second rule.
But d(1) fails. And there's no way we can resatisfy the goal p(X). Sure, if we were allowed to try the value X=2 we could use the second rule to generate a solution (that's what happened in the original version of the program). But we can't do this: the cut has committed us to the choice X=1. And sure, if we were allowed to try the third rule, we could generate the solution X=3. But we can't do this: the cut has committed us to using the second rule.

Looking at the search tree this means that search stops when the goal d(1) cannot be shown as going up the tree doesn't lead us to any node where an alternative choice is available. The red nodes in the tree are all blocked for backtracking because of the cut.

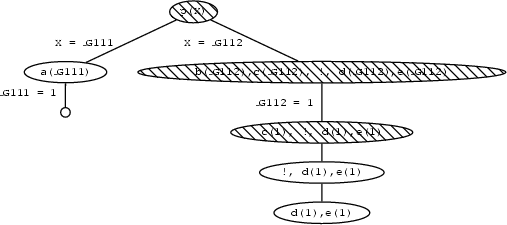
One point is worth emphasizing: the cut only commits us to choices made since the parent goal was unified with the left hand side of the clause containing the cut. For example, in a rule of the form

q :- p1,...,pn,!,r1,...,rm

once we reach the the cut, it commits us to using this particular clause for q and it commits us to the choices made when evalauting p1,...,pn. However, we are free to backtrack among the r1,...,rm and we are also free to backtrack among alternatives for choices that were made before reaching the goal q. Concrete examples will make this clear.

First consider the following cut-free program:

s(X,Y) :- q(X,Y). s(0,0). q(X,Y) :- i(X),j(Y). i(1). i(2). j(1). j(2). j(3).

Here's how it behaves:

?- s(X,Y). X = 1 Y = 1 ; X = 1 Y = 2 ; X = 1 Y = 3 ; X = 2 Y = 1 ; X = 2 Y = 2 ; X = 2 Y = 3 ; X = 0 Y = 0; no

Suppose we add a cut to the clause defining q/2:

q(X,Y) :- i(X),!,j(Y).

Now the program behaves as follows:

?- s(X,Y). X = 1 Y = 1 ; X = 1 Y = 2 ; X = 1 Y = 3 ; X = 0 Y = 0; no

Let's see why.

s(X,Y) is first matched with the first rule, which gives us a new goal q(X,Y).
q(X,Y) is then matched with the third rule, so we get the new goals i(X),!,j(Y). By instantiating X to 1, Prolog matches i(X) with the fact i(1). This leaves us with the goal !,j(Y). The cut, of course, succeeds, and commits us to the choices so far made.
But what are these choices? These: that X = 1, and that we are using this clause. But note: we have not yet chosen a value for Y.
Prolog then goes on, and by instantiating Y to 1, Prolog matches j(Y) with the fact j(1). So we have found a solution.
But we can find more. Prolog is free to try another value for Y. So it backtracks and sets Y to 2, thus finding a second solution. And in fact it can find another solution: on backtracking again, it sets Y to 3, thus finding a third solution.
But those are all alternatives for j(X). Backtracking to the left of the cut is not allowed, so it can't reset X to 2, so it won't find the next three solutions that the cut-free program found. Backtracking over goals that were reached before q(X,Y) is allowed however, so that Prolog will find the second clause for s/2.

Looking at it in terms of the search tree, this means that all nodes above the cut up to the one containing the goal that led to the selection of the clause containing the cut are blocked.

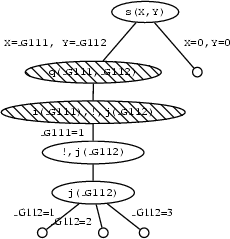
Well, we now know what cut is. But how do we use it in practice, and why is it so useful? As a first example, let's define a (cut-free) predicate max/3 which takes integers as arguments and succeeds if the third argument is the maximum of the first two. For example, the queries

max(2,3,3)

and

max(3,2,3)

and

max(3,3,3)

should succeed, and the queries

max(2,3,2)

and

max(2,3,5)

should fail. And of course, we also want the program to work when the third argument is a variable. That is, we want the program to be able to find the maximum of the first two arguments for us:

?- max(2,3,Max). Max = 3 Yes ?- max(2,1,Max). Max = 2 Yes

Now, it is easy to write a program that does this. Here's a first attempt:

max(X,Y,Y) :- X =< Y. max(X,Y,X) :- X>Y.

This is a perfectly correct program, and we might be tempted simply to stop here. But we shouldn't: it's not good enough. What's the problem? There is a potential inefficiency. Suppose this definition is used as part of a larger program, and somewhere along the way max(3,4,Y) is called. The program will correctly set Y=4. But now consider what happens if at some stage backtracking is forced. The program will try to resatisfy max(3,4,Y) using the second clause. And of course, this is completely pointless: the maximum of 3 and 4 is 4 and that's that. There is no second solution to find. To put it another way: the two clauses in the above program are mutually exclusive: if the first succeeds, the second must fail and vice versa. So attempting to resatisfy this clause is a complete waste of time.

With the help of cut, this is easy to fix. We need to insist that Prolog should never try both clauses, and the following code does this:

max(X,Y,Y) :- X =< Y,!. max(X,Y,X) :- X>Y.

Note how this works. Prolog will reach the cut if max(X,Y,Y) is called and X =< Y succeeds. In this case, the second argument is the maximum, and that's that, and the cut commits us to this choice. On the other hand, if X =< Y fails, then Prolog goes onto the second clause instead.

Note that this cut does not change the meaning of the program. Our new code gives exactly the same answers as the old one, it's just a bit more efficient. In fact, the program is exactly the same as the previous version, except for the cut, and this is a pretty good sign that the cut is a sensible one. Cuts like this, which don't change the meaning of a program, have a special name: they're called green cuts.

But there is another kind of cut: cuts which do change the meaning of a program. These are called red cuts, and are usually best avoided. Here's an example of a red cut. Yet another way to write the max predicate is as follows:

max(X,Y,Y) :- X =< Y,!. max(X,Y,X).

This is the same as our earlier green cut max, except that we have got rid of the > test in the second clause. This is bad sign: it suggests that we're changing the underyling logic of the program. And indeed we are: this program `works' by relying on cut. How good is it?

Well, for some kinds of query it's fine. In particular, it answers correctly when we pose queries in which the third argument is a variable. For example:

?- max(100,101,X). X = 101 Yes

and

?- max(3,2,X). X = 3 Yes

Nonetheless, it's not the same as the green cut program: the meaning of max has changed. Consider what happens when all three arguments are instantiated. For example, consider the query

max(2,3,2).

Obviously this query should fail. But in the red cut version, it will succeed! Why? Well, this query simply won't match the head of the first clause, so Prolog goes straight to the second clause. And the query will match with the second clause, and (trivially) the query succeeds! Oops! Getting rid of that > test wasn't quite so smart after all...

This program is a classic red cut. It does not truly define the max predicate, rather it changes it's meaning and only gets things right for certain types of queries.

A sensible way of using cut is to try and get a good, clear, cut free program working, and only then try to improve its efficiency using cuts. It's not always possible to work this way, but it's a good ideal to aim for.