8.1.2 Building parse trees

So far, the programs we have discussed have been able to recognize grammatical structure (that is, they could correctly answer ``yes'' or ``no'' when asked whether the input was a sentence, a noun phrase, and so on) and to generate grammatical output. This is pleasant, but we would also like to be able to parse. That is, we would like our programs not only to tell us which sentences are grammatical, but also to give us an analysis of their structure. In particular, we would like to see the trees the grammar assigns to sentences.

Well, using only standard Prolog tool we can't actually draw nice pictures of trees, but we can build data structures which describe trees in a clear way. For example, corresponding to the tree

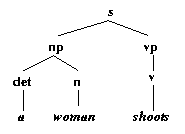
we could have the following term:

s(np(det(a),n(woman)),vp(v(shoots))).

Sure: it doesn't look as nice, but all the information in the picture is there. And, with the aid of a decent graphics package, it would be easy to turn this term into a picture.

But how do we get DCGs to build such terms? Actually, it's pretty easy. After all, in effect a DCG has to work out what the tree structure is when recognizing a sentence. So we just need to find a way of keeping track of the structure that the DCG finds. We do this by adding extra arguments. Here's how:

s(s(NP,VP)) --> np(NP),vp(VP).
 
np(np(DET,N)) --> det(DET),n(N).
 
vp(vp(V,NP)) --> v(V),np(NP).
vp(vp(V))    --> v(V).
 
det(det(the)) --> [the].
det(det(a))   --> [a].
 
n(n(woman)) --> [woman].
n(n(man))   --> [man].
 
v(v(shoots)) --> [shoots].

What's going on here? Essentially we are building the parse trees for the syntactic categories on the left-hand side of the rules out of the parse trees for the syntactic categories on the right-hand side of the rules. Consider the rule vp(vp(V,NP)) --> v(V),np(NP). When we make a query using this DCG, the V in v(V) and the NP in np(NP) will be instantiated to terms representing parse trees. For example, perhaps V will be instantiated to

v(shoots)

and NP will be instantiated to

np(det(a),n(woman)).

What is the term corresponding to a vp made out of these two structures? Obviously it should be this:

vp(v(shoots),np(det(a),n(woman))).

And this is precisely what the extra argument vp(V,NP) in the rule vp(vp(V,NP)) --> v(V),np(NP) gives us: it forms a term whose functor is vp, and whose first and second arguments are the values of V and NP respectively. To put it informally: it plugs the V and the NP terms together under a vp functor.

To parse the sentence ``A woman shoots'' we pose the query:

s(T,[a,woman,shoots],[]).

That is, we ask for the extra argument T to be instantiated to a parse tree for the sentence. And we get:

T = s(np(det(a),n(woman)),vp(v(shoots)))  
yes

Furthermore, we can generate all parse trees by making the following query:

s(T,S,[]).

The first three responses are:

T = s(np(det(the),n(woman)),vp(v(shoots),np(det(the),n(woman))))  
S = [the,woman,shoots,the,woman] ;
 
T = s(np(det(the),n(woman)),vp(v(shoots),np(det(the),n(man))))  
S = [the,woman,shoots,the,man] ;
 
T = s(np(det(the),n(woman)),vp(v(shoots),np(det(a),n(woman))))  
S = [the,woman,shoots,a,woman] 

This code should be studied closely: it's a classic example of building structure using unification.

Extra arguments can also be used to build semantic representations. We did not say anything about what the words in our little DCG mean. In fact, nowadays a lot is known about the semantics of natural languages, and it is surprisingly easy to build semantic representations which partially capture the meaning of sentences or entire discourses. Such representations are usually expressions of some formal language (for example first-order logic, discourse representation structures, or a database query language) and they are usually built up compositionally. That is, the meaning of each word is expressed in the formal language; this meaning is given as an extra argument in the DCG entries for the individual words. Then, for each rule in the grammar, an extra argument shows how to combine the meaning of the two subcomponents. For example, to the rule s --> np, vp we would add an extra argument stating how to combine the np meaning and the vp meaning to form the s meaning. Although somewhat more complex, the semantic construction process is quite like the way we built up the parse tree for the sentence from the parse tree of its subparts.