7.4 Practical Session 7

The purpose of Practical Session 7 is to help you get familiar with the DCGs, difference lists, and the relation between them, and to give you some experience in writing basic DCGs. As you will learn next week, there is more to DCGs than the ideas just discussed. Nonetheless, what you have learned so far is certainly the core, and it is important that you are comfortable with the basic ideas before moving on.

First some keyboard exercises:

First, type in or download the simple append based recognizer discussed in the text, and then run some traces. As you will see, we were not exaggerating when we said that the performance of the append based grammar was very poor. Even for such simple sentences as The woman shot a man you will see that the trace is very long, and very difficult to follow.
Next, type in or download our second recognizer, the one based on difference lists, and run more traces. As you will see, there is a dramatic gain in efficiency. Moreover, even if you find the idea of difference lists a bit hard to follow, you will see that the traces are very simple to understand, especially when compared with the monsters produced by the append based implementation!
Next, type in or download the DCG discussed in the text. Type listing so that you can see what Prolog translates the rules to. How does your system translate rules of the form Det --> [the]? That is, does it translate them to rules like det([the|X],X), or does is make use of rules containing the 'C'predicate?
Now run some traces. Apart from variable names, the traces you observe here should be very similar to the traces you observed when running the difference list recognizer. In fact, you will only observe any real differences if your version of Prolog uses a 'C' based translation.

And now it's time to write some DCGs:

The formal language aEven is very simple: it consists of all strings containing an even number of as, and nothing else. Note that the empty string $\epsilon$ belongs to aEven. Write a DCG that generates aEven.
The formal language 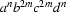$a^nb^{2m}c^{2m}d^{n}$ consists of all strings of the following form: an unbroken block of as followed by an unbroken block of bs followed by an unbroken block of cs followed by an unbroken block of ds, such that the a and d blocks are exactly the same length, and the c and d blocks are also exactly the same length and furthermore consist of an even number of cs and ds respectively. 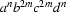For example, $\epsilon$ , abbccd, and aaabbbbccccddd all belong to $a^nb^{2m}c^{2m}d^{n}$ . Write a DCG that generates this language.
The language that logicians call `propositional logic over the propositional symbols p, q, and r' can be defined by the following context free grammar:
prop -> p
prop -> q
prop -> r
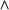
prop -> $\neg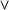$ prop
prop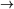 -> (prop $\wedge$ prop)
prop -> (prop $\vee$ prop)
prop -> (prop $\rightarrow$ prop)
Write a DCG that generates this language. Actually, because we don't know about Prolog operators yet, you will have to make a few rather clumsy looking compromises. For example, instead of getting it to recognize
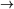
$\neg$ (p $\rightarrow$ q)
you will have to get it recognize things like
[not, '(', p, implies, q, ')']
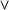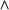instead. But we will learn later how to make the output nicer, so write the DCG that accepts a clumsy looking version of this language. Use or for $\vee$ , and and for $\wedge$ .