7.1 Context free grammars
Prolog has been used for many purposes, but its inventor, Alain Colmerauer, was a computational linguist, and computational linguistics remains a classic application for the language. Moreover, Prolog offers a number of tools which make life easier for computational linguists, and today we are going to start learning about one of the most useful of these: Definite Clauses Grammars, or DCGs as they are usually called.
DCGs are a special notation for defining grammars. So, before we go any further, we'd better learn what a grammar is. We shall do so by discussing context free grammars (or CFGs). The basic idea of context free grammars is simple to understand, but don't be fooled into thinking that CFGs are toys. They're not. While CFGs aren't powerful enough to cope with the syntactic structure of all natural languages (that is, the kind of languages that human beings use), they can certainly handle most aspects of the syntax of many natural languages (for example, English, German, and French) in a reasonably natural way.
So what is a context free grammar? In essence, a finite collection of rules which tell us that certain sentences are grammatical (that is, syntactically correct) and what their grammatical structure actually is. Here's a simple context free grammar for a small fragment of English:
|
|
|
|
|
|
|
|
|
What are the ingredients of this little grammar? Well, first note that it contains three types of symbol. There's ->, which is used to define the rules. Then there are the symbols written like this: s, np, vp, det, n, v. These symbols are called non-terminal symbols; we'll soon learn why. Each of these symbols has a traditional meaning in linguistics: s is short for sentence, np is short for noun phrase, vp is short for verb phrase, and det is short for determiner. That is, each of these symbols is shorthand for a grammatical category. Finally there are the symbols in italics: a, the, woman, man, and shoots. A computer scientist would probably call these terminal symbols (or: the alphabet), and linguists would probably call them lexical items. We'll use these terms occasionally, but often we'll make life easy for ourselves and just call them words.
Now, this grammar contains nine rules. A context free rule consists of a single non-terminal symbol, followed by ->, followed by a finite sequence made up of terminal and/or non-terminal symbols. All nine items listed above have this form, so they are all legitimate context free rules. What do these rules mean? They tell us how different grammatical categories can be built up. Read -> as can consist of, or can be built out of. For example, the first rule tells us that a sentence can consist of a noun phrase followed by a verb phrase. The third rule tells us that a verb phrase can consist of a verb followed by a noun phrase, while the fourth rule tells us that there is another way to build a verb phrase: simply use a verb. The last five rules tell us that a and the are determiners, that man and woman are nouns, and that shoots is a verb.
Now, consider the string of words a woman shoots a man. Is this grammatical according to our little grammar? And if it is, what structure does it have? The following tree answers both questions:
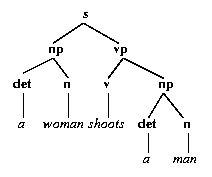
Right at the top we have a node marked s. This node has two daughters, one marked np, and one marked vp. Note that this part of the diagram agrees with the first rule of the grammar, which says that an s can be built out of an np and a vp. (A linguist would say that this part of the tree is licensed by the first rule.) In fact, as you can see, every part of the tree is licensed by one of our rules. For example, the two nodes marked np are licensed by the rule that says that an np can consist of a det followed by an n. And, right at the bottom of the diagram, all the words in a woman shoots a man are licensed by a rule. Incidentally, note that the terminal symbols only decorate the nodes right at the bottom of the tree (the terminal nodes) while non-terminal symbols only decorate nodes that are higher up in the tree (the non-terminal nodes).
Such a tree is called a parse tree, and it gives us two sorts of information: information about strings and information about structure. This is an important distinction to grasp, so let's have a closer look, and learn some important terminology while we are doing so.
First, if we are given a string of words, and a grammar, and it turns out that we can build a parse tree like the one above (that is, a tree that has s at the top node, and every node in the tree is licensed by the grammar, and the string of words we were given is listed in the correct order along the terminal nodes) then we say that the string is grammatical (according to the given grammar). For example, the string a woman shoots a man is grammatical according to our little grammar (and indeed, any reasonable grammar of English would classify it as grammatical). On the other hand, if there isn't any such tree, the string is ungrammatical (according to the given grammar). For example, the string woman a woman man a shoots is ungrammatical according to our little grammar (and any reasonable grammar of English would classify it as ungrammatical). The language generated by a grammar consists of all the strings that the grammar classifies as grammatical. For example, a woman shoots a man also belongs to the language generated by our little grammar, and so does a man shoots the woman. A context free recognizer is a program which correctly tells us whether or not a string belongs to the language generated by a context free grammar. To put it another way, a recognizer is a program that correctly classifies strings as grammatical or ungrammatical (relative to some grammar).
But often, in both linguistics and computer science, we are not merely interested in whether a string is grammatical or not, we want to know why it is grammatical. More precisely, we often want to know what its structure is, and this is exactly the information a parse tree gives us. For example, the above parse tree shows us how the words in a woman shoots a man fit together, piece by piece, to form the sentence. This kind of information would be important if we were using this sentence in some application and needed to say what it actually meant (that is, if we wanted to do semantics). A context free parser is a program which correctly decides whether a string belongs to the language generated by a context free grammar and also tells us hat its structure is. That is, whereas a recognizer merely says `Yes, grammatical' or `No, ungrammatical' to each string, a parser actually builds the associated parse tree and gives it to us.
It remains to explain one final concept, namely what a context free language is. (Don't get confused: we've told you what a context free grammar is, but not what a context free language is.) Quite simply, a context free language is a language that can be generated by a context free grammar. Some languages are context free, and some are not. For example, it seems plausible that English is a context free language. That is, it is probably possible to write a context free grammar that generates all (and only) the sentences that native speakers find acceptable. On the other hand, some dialects of Swiss-German are not context free. It can be proved mathematically that no context free grammar can generate all (and only) the sentences that native speakers find acceptable. So if you wanted to write a grammar for such dialects, you would have to employ additional grammatical mechanisms, not merely context free rules.