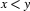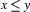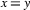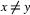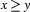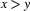5.4 Comparing integers

Some Prolog arithmetic predicates actually do carry out arithmetic all by themselves (that is, without the assistance of is). These are the operators that compare integers.

These operators have the obvious meaning:

2 < 4.
yes
 
2 =< 4.
yes
 
4 =< 4.
yes
 
4=:=4.
yes
 
4=\=5.
yes
 
4=\=4.
no
 
4 >= 4.
yes
 
4 > 2.
yes

Moreover, they force both their right-hand and left-hand arguments to be evaluated:

2 < 4+1.
yes
 
2+1 < 4.
yes
 
2+1 < 3+2.
yes

Note that =:= really is different from =, as the following examples show:

4=4.
yes
 
2+2 =4.
no
 
2+2 =:= 4.
yes

That is, = tries to unify its arguments; it does not force arithmetic evaluation. That's =:='s job.

Whenever we use these operators, we have to take care that any variables are instantiated. For example, all the following queries lead to instantiation errors.

X < 3.
 
3 < Y.
 
X =:= X.

Moreover, variables have to be instantiated to integers. The query

X = 3, X < 4.

succeeds. But the query

X = b, X < 4.

fails.

OK, let's now look at an example which puts Prolog's abilities to compare numbers to work. We're going to define a predicate which takes takes a list of non-negative integers as its first argument, and returns the maximum integer in the list as its last argument. Again, we'll use an accumulator. As we work our way down the list, the accumulator will keep track of the highest integer found so far. If we find a higher value, the accumulator will be updated to this new value. When we call the program, we set accumulator to an initial value of 0. Here's the code. Note that there are two recursive clauses:

accMax([H|T],A,Max) :-
    H > A,
    accMax(T,H,Max).
 
accMax([H|T],A,Max) :-
    H =< A,
    accMax(T,A,Max).
 
accMax([],A,A).

The first clause tests if the head of the list is larger than the largest value found so far. If it is, we set the accumulator to this new value, and then recursively work through the tail of the list. The second clause applies when the head is less than or equal to the accumulator; in this case we recursively work through the tail of the list using the old accumulator value. Finally, the base clause unifies the second and third arguments; it gives the highest value we found while going through the list to the last argument. Here's how it works:

accMax([1,0,5,4],0,_5810)  
 
accMax([0,5,4],1,_5810)  
 
accMax([5,4],1,_5810)  
 
accMax([4],5,_5810)  
 
accMax([],5,_5810)  
 
accMax([],5,5) 

Again, it's nice to define a predicate which calls this, and initializes the accumulator. But wait: what should we initialize the accumulator too? If you say 0, this means you are assuming that all the numbers in the list are positive. But suppose we give a list of negative integers as input. Then we would have

accMax([-11,-2,-7,-4,-12],0,Max).
 
Max = 0  
yes

This is not what we want: the biggest number on the list is -2. Our use of 0 as the initial value of the accumulator has ruined everything, because it's bigger than any number on the list.

There's an easy way around this: since our input list will always be a list of integers, simply initialize the accumulator to the head of the list. That way we guarantee that the accumulator is initialized to a number on the list. The following predicate does this for us:

max(List,Max) :-  
     List = [H|_],
     accMax(List,H,Max).

So we can simply say:

max([1,2,46,53,0],X).
 
X = 53
yes

And furthermore we have:

max([-11,-2,-7,-4,-12],X).
 
X = -2  
yes