3.1.4 Example 3: Addition

As a final example, let's see whether we can use the representation of numerals that we introduced in the previous section for doing simple arithmetic. Let's try to define addition. That is, we want to define a predicate add/3 which when given two numerals as the first and second argument returns the result of adding them up as its third argument. E.g.

?- add(succ(succ(0)),succ(succ(0)),succ(succ(succ(succ(0))))). yes ?- add(succ(succ(0)),succ(0),Y). Y = succ(succ(succ(0)))

There are two things which are important to notice:

Whenever the first argument is 0, the third argument has to be the same as the second argument:
?- add(0,succ(succ(0)),Y). Y = succ(succ(0)) ?- add(0,0,Y). Y = 0
This is the case that we want to use for the base clause.
Assume that we want to add the two numerals X and Y (e.g. succ(succ(succ(0))) and succ(succ(0))) and that X is not 0. Now, if X' is the numeral that has one succ functor less than X (i.e. succ(succ(0)) in our example) and if we know the result -- let's call it Z -- of adding X' and Y (namely succ(succ(succ(succ(0))))), then it is very easy to compute the result of adding X and Y: we just have to add one succ-functor to Z. This is what we want to express with the recursive clause.

Here is the predicate definition that expresses exactly what we just said:

add(0,Y,Y). add(succ(X),Y,succ(Z)) :- add(X,Y,Z).

So, what happens, if we give Prolog this predicate definition and then ask:

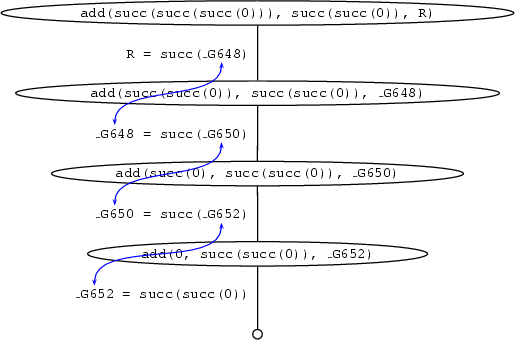
add(succ(succ(succ(0))), succ(succ(0)), R)

Let's go through the way Prolog processes this query step by step. The trace and the search tree are given below.

The first argument is not 0 which means that only the second clause for add matches. This leads to a recursive call of add. The outermost succ functor is stripped off the first argument of the original query, and the result becomes the first argument of the recursive query. The second argument is just passed on to the recursive query, and the third argument of the recursive query is a variable, the internal variable _G648 in the trace given below. _G648 is not instantiated, yet. However, it is related to R (which is the variable that we had as third argument in the original query), because R was instantiated to succ(_G648), when the query was matched to the head of the second clause. But that means that R is not a completely uninstantiated variable anymore. It is now a complex term, that has a (uninstantiated) variable as its argument.

The next two steps are essentially the same. With every step the first argument becomes one level smaller. The trace and the search tree show this nicely. At the same time one succ functor is added to R with every step, but always leaving the argument of the innermost variable uninstantiated. After the first recursive call R is succ(_G648), in the second recursive call _G648 is instantiated with succ(_G650), so that R is succ(succ(_G650), in the third recursive call _G650 is instantiated with succ(_G652) and R therefore becomes succ(succ(succ(_G652))). The search tree shows this step by step instantiation.

At some point all succ functors have been stripped off the first argument and we have reached the base clause. Here, the third argument is equated with the second argument, so that "the hole" in the complex term R is finally filled.

This is a trace for the query add(succ(succ(succ(0))), succ(succ(0)), R):

Call: (6) add(succ(succ(succ(0))), succ(succ(0)), R) Call: (7) add(succ(succ(0)), succ(succ(0)), _G648) Call: (8) add(succ(0), succ(succ(0)), _G650) Call: (9) add(0, succ(succ(0)), _G652) Exit: (9) add(0, succ(succ(0)), succ(succ(0))) Exit: (8) add(succ(0), succ(succ(0)), succ(succ(succ(0)))) Exit: (7) add(succ(succ(0)), succ(succ(0)), succ(succ(succ(succ(0))))) Exit: (6) add(succ(succ(succ(0))), succ(succ(0)), succ(succ(succ(succ(succ(0))))))

And here is the search tree for this query: