3.1.2 Example 2: Descendant

Now that we know something about what recursion in Prolog involves, it is time to ask why it is so important. Actually, this is a question that can be answered on a number of levels, but for now, let's keep things fairly practical. So: when it comes to writing useful Prolog programs, are recursive definitions really so important? And if so, why?

Let's consider an example. Suppose we have a knowledge base recording facts about the child relation:

child(charlotte,caroline). child(caroline,laura).

That is, Caroline is a child of Charlotte, and Laura is a child of Caroline. Now suppose we wished to define the descendant relation; that is, the relation of being a child of, or a child of a child of, or a child of a child of a child of, or.... Here's a first attempt to do this. We could add the following two non-recursive rules to the knowledge base:

descend(X,Y) :- child(X,Y). descend(X,Y) :- child(X,Z), child(Z,Y).

Now, fairly obviously these definitions work up to a point, but they are clearly extremely limited: they only define the concept of descendant-of for two generations or less. That's ok for the above knowledge base, but suppose we get some more information about the child-of relation and we expand our list of child-of facts to this:

child(martha,charlotte). child(charlotte,caroline). child(caroline,laura). child(laura,rose).

Now our two rules are inadequate. For example, if we pose the queries

?- descend(martha,laura).

?- descend(charlotte,rose).

we get the answer `No!', which is not what we want. Sure, we could `fix' this by adding the following two rules:

descend(X,Y) :- child(X,Z_1), child(Z_1,Z_2), child(Z_2,Y). descend(X,Y) :- child(X,Z_1), child(Z_1,Z_2), child(Z_2,Z_3), child(Z_3,Y).

But, let's face it, this is clumsy and hard to read. Moreover, if we add further child-of facts, we could easily find ourselves having to add more and more rules as our list of child-of facts grow, rules like:

descend(X,Y) :- child(X,Z_1), child(Z_1,Z_2), child(Z_2,Z_3), . . . child(Z_17,Z_18). child(Z_18,Z_19). child(Z_19,Y).

This is not a particularly pleasant (or sensible) way to go!

But we don't need to do this at all. We can avoid having to use ever longer rules entirely. The following recursive rule fixes everything exactly the way we want:

descend(X,Y) :- child(X,Y). descend(X,Y) :- child(X,Z), descend(Z,Y).

What does this say? The declarative meaning of the base clause is: if Y is a child of X, then Y is a descendant of X. Obviously sensible.

So what about the recursive clause? It's declarative meaning is: if Z is a child of X, and Y is a descendant of Z, then Y is a descendant of X. Again, this is obviously true.

So let's now look at the procedural meaning of this recursive predicate, by stepping through an example. What happens when we pose the query:

descend(martha,laura)

Prolog first tries the first rule. The variable X in the head of the rule is unified with martha and Y with laura and the next goal Prolog tries to prove is

child(martha,laura)

This attempt fails, however, since the knowledge base neither contains the fact child(martha,laura) nor any rules that would allow to infer it. So Prolog backtracks and looks for an alternative way of proving descend(martha,laura). It finds the second rule in the knowledge base and now has the following subgoals:

child(martha,_633), descend(_633,laura).

Prolog takes the first subgoal and tries to match it onto something in the knowledge base. It finds the fact child(martha,charlotte) and the Variable _633 gets instantiated to charlotte. Now that the first subgoal is satisfied, Prolog moves to the second subgoal. It has to prove

descend(charlotte,laura)

This is the recursive call of the predicate descend/2. As before, Prolog starts with the first rule, but fails, because the goal

child(charlotte,laura)

cannot be proved. Backtracking, Prolog finds that there is a second possibility to be checked for descend(charlotte,laura), viz. the second rule, which again gives Prolog two new subgoals:

child(charlotte,_1785), descend(_1785,laura).

The first subgoal can be unified with the fact child(charlotte,caroline) of the knowledge base, so that the variable _1785 is instantiated with caroline. Next Prolog tries to prove

descend(caroline,laura).

This is the second recursive call of predicate descend/2. As before, it tries the first rule first, obtaining the following new goal:

child(caroline,laura)

This time Prolog succeeds, since child(caroline,laura) is a fact in the database. Prolog has found a proof for the goal descend(caroline,laura) (the second recursive call). But this means that child(charlotte,laura) (the first recursive call) is also true, which means that our original query descend(martha,laura) is true as well.

Here is the search tree for the query descend(martha,laura). Make sure that you understand how it relates to the discussion in the text; i.e. how Prolog traverses this search tree when trying to prove this query.

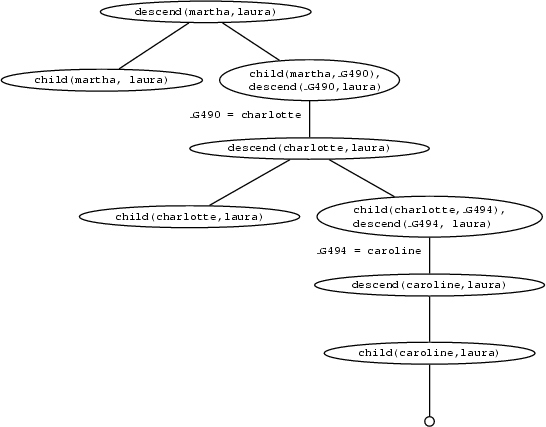
It should be obvious from this example that no matter how many generations of children we add, we will always be able to work out the descendant relation. That is, the recursive definition is both general and compact: it contains all the information in the previous rules, and much more besides. In particular, the previous lists of non-recursive rules only defined the descendant concept up to some fixed number of generations: we would need to write down infinitely many non-recursive rules if we wanted to capture this concept fully, and of course that's impossible. But, in effect, that's what the recursive rule does for us: it bundles up all this information into just three lines of code.

Recursive rules are really important. They enable to pack an enormous amount of information into a compact form and to define predicates in a natural way. Most of the work you will do as a Prolog programmer will involve writing recursive rules.