2.2 Proof Search

Now that we know about matching, we are in a position to learn how Prolog actually searches a knowledge base to see if a query is satisfied. That is, we are now able to learn about proof search. We will introduce the basic ideas involved by working through a simple example.

Suppose we are working with the following knowledge base

f(a). f(b). g(a). g(b). h(b). k(X) :- f(X),g(X),h(X).

Suppose we then pose the query

k(X).

You will probably see that there is only one answer to this query, namely k(b), but how exactly does Prolog work this out? Let's see.

Prolog reads the knowledge base, and tries to match k(X) with either a fact, or the head of a rule. It searches the knowledge base top to bottom, and carries out the matching, if it can, at the first place possible. Here there is only one possibility: it must match k(X) to the head of the rule k(X) :- f(X),g(X),h(X).

When Prolog matches the variable in a query to a variable in a fact or rule, it generates a brand new variable to represent that the variables are now sharing. So the original query now reads:

k(_G348)

and Prolog knows that

k(_G348) :- f(_G348),g(_G348),h(_G348).

So what do we now have? The query says: `I want to find an individual that has property k'. The rule says,`an individual has property k if it has properties f, g, and h'. So if Prolog can find an individual with properties f, g, and h, it will have satisfied the original query. So Prolog replaces the original query with the following list of goals:

f(_G348),g(_G348),h(_G348).

We will represent this graphically as

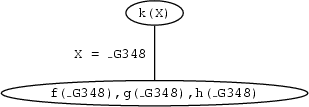
That is, our original goal is to prove k(X). When matching it with the head of the rule in the knowledge base X and the internal variable _G348 are made equal and we are left with the goals f(_G348),g(_G348),h(_G348).

Now, whenever it has a list of goals, Prolog tries to satisfy them one by one, working through the list in a left to right direction. The leftmost goal is f(_G348), which reads: `I want an individual with property f'. Can this goal be satisfied? Prolog tries to do so by searching through the knowledge base from top to bottom. The first thing it finds that matches this goal is the fact f(a). This satisfies the goal f(_G348) and we are left with two more goals to go. When matching f(_G348) to f(a), X is instantiated to a. This applies to all occurrences of X in the list of goals. So, the list of remaining goals is:

g(a),h(a)

and our graphical representation of the proof search looks like this:

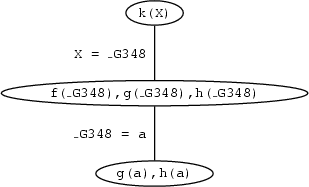
The fact g(a) is in the knowledge base. So the next goal we have to prove is satisfied too, and the goal list is now

h(a)

and the graphical representation

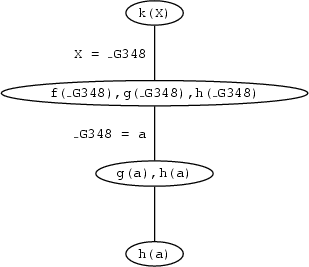
But there is no way to satisfy this goal. The only information h we have in the knowledge base is h(b) and this won't match h(a).

So Prolog decides it has made a mistake and checks whether at some point there was another possibility for matching a goal with a fact or the head of a rule in the knowledge base. It does this by going back up the path in the graphical representation that it was coming down on. There is nothing else in the knowledge base that matches with g(a), but there is another possibility for matching f(_G348). Points in the search where there are several alternatives for matching a goal against the knowledge base are called choice points. Prolog keeps track of choice points and the choices that it has made there, so that if it makes a wrong choice, it can go back to the choice point and try something else. This is called backtracking.

So, Prolog backtracks to the last choice point, where the list of goals was:

f(_G348),g(_G348),h(_G348).

Prolog has to redo all this. Prolog tries to resatisfy the first goal, by searching further in the knowledge base. It sees that it can match the first goal with information in the knowledge base by matching f(_G348) with f(b). This satisfies the goal f(_G348) and instantiates X to b, so that the remaining goal list is

g(b),h(b).

But g(b) is a fact in the knowledge base, so this is satisfied too, leaving the goal list:

h(b).

And this fact too is in the knowledge base, so this goal is also satisfied. Important: Prolog now has an empty list of goals. This means that it has proved everything it had to to establish the original goal, namely k(X). So this query is satisfiable, and moreover, Prolog has also discovered what it has to do to satisfy it, namely instantiate X to b.

Representing these last steps graphically gives us

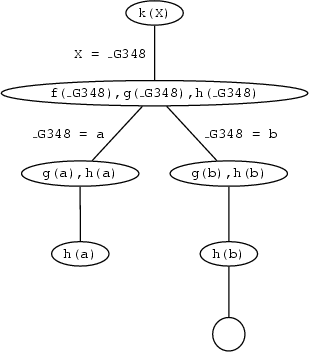
It is interesting to consider what happens if we then ask for another solution by typing:

;

This forces Prolog to backtrack to the last choice point, to try and find another possibility. However, there is no other choice point, as there are no other possibilities for matching h(b), g(b), f(_G348), or k(X) with clauses in the knowledge base. So at this point Prolog would correctly have said `no'. Of course, if there had been other rules involving k, Prolog would have gone off and tried to use them in exactly the way we have described: that is, by searching top to bottom in the knowledge base, left to right in goal lists, and backtracking to the previous choice point whenever it fails.

Now, look at the graphical representation that we built while searching for proofs of k(X). It is a tree structure. The nodes of the tree say which are the goals that have to be satisfied at a certain point during the search and at the edges we keep track of the variable instantiations that are made when the current goal (i.e. the first one in the list of goals) is match to a fact or the head of a rule in the knowledge base. Such trees are called search trees and they are a nice way of visualizing the steps that are taken in searching for a proof of some query. Leave nodes which still contain unsatisfied goals are point where Prolog failed, because it made a wrong decision somewhere along the path. Leave nodes with an empty goal list, correspond to a possible solution. The information on the edges along the path from the root node to that leave tell you what are the variable instantiations with which the query is satisfied.

Let's have a look at another example. Suppose that we are working with the following knowledge base:

loves(vincent,mia). loves(marcellus,mia). jealous(X,Y) :- loves(X,Z),loves(Y,Z).

Now, we pose the query

jealous(X,Y).

The search tree for this query looks like this:

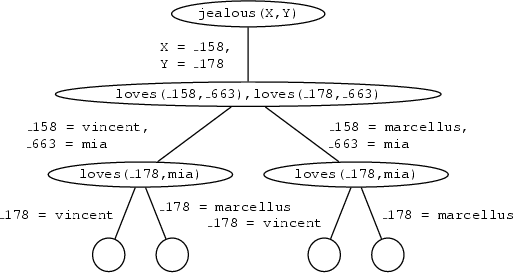
There is only one possibility of matching jealous(X,Y) against the knowledge base. That is by using the rule

jealous(X,Y) :- loves(X,Z),loves(Y,Z).

The new goals that have to be satisfied are then

loves(_G100,_G101),loves(_G102,_G101)

Now, we have to match loves(_G100,_G101) against the knowledge base. There are two ways of how this can be done: it can either be matched with the first fact or with the second fact. This is why the path branches at this point. In both cases the goal loves(_G102,mia) is left, which also has two possibilities of how it can be satisfied, namely the same ones as above. So, we have four leave nodes with an empty goal list, which means that there are four ways for satisfying the query. The variable instantiation for each of them can be read off the path from the root to the leaf node. They are

X = \_158 = vincent and Y = \_178 = vincent
X = \_158 = vincent and Y = \_178 = marcellus
X = \_158 = marcellus and Y = \_178 = vincent
X = \_158 = marcellus and Y = \_178 = marcellus