In the last lesson, we saw how complicated it was to try and teach Reeborg to add two numbers. In this lesson, we will see how easy it is to get to add numbers using the Python language... and do other mathematical operations.
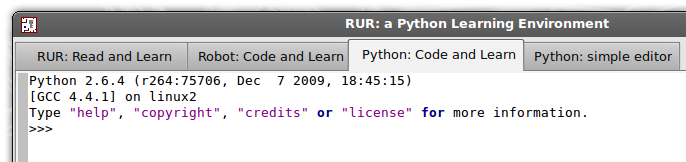
Select the Python interpreter (Python: Code and Learn), by clicking on the third tab. Your display should look something like the following:
Ignore the first two lines of the display for now. On the third line is the Python prompt
>>>
The Python prompt is the Python program waiting for you to input some command. Now, let's see if we can make Python add two numbers more easily than Reeborg could. Put the cursor on line 3 to the right of the prompt, click to select it and type:
8 and 4
Then you press the Enter key to tell the Python interpreter (the program that handles your Python statements), that you are ready, and it is now able to process your entry. Python will reply, in its own language, in what may appears as some insults!
>>>Add 8 and 4 File "<input>", line 1 Add 8 and 4 ^ SyntaxError: invalid syntax >>>
So, the Python interpreter does not understand commands written in English. However, you should note that it does recognize Python keywords like and as it displays them in a different color than the rest of the text (different also from the color we have chosen, but that is not important.)
Note that it is prompting you again for some new input. This time, try something simpler like typing "8+4" followed by the "enter" key. You should see something like this on the display:
>>> 8+4 12 >>>
Success! Python added the two numbers right away (which was so difficult to get Reeborg to do). It's even prompting you again to give it more instructions. You can try something like the following, which I have copied from the interpreter to here.
>>> 8+4 12 >>> 8-4 4 >>> 8*4 32 >>> 8/4 2
As you can see, Python knows how to add, subtract, multiply and divide.
Python knows about the order of precedence of mathematical operators. By this we mean that, when you have many numbers and mathematical operations, you multiply and divide numbers first (from left to right), then add and subtract, etc. Here, a few examples are probably a better explanation than words could provide on their own.
>>> 2+3*5
17
>>> 2+ (3*5) # Python does not care about spaces here
17
>>> (2+3)*5
25
>>> 2*4/8
1
>>> 2+1-4
-1
Go ahead, try some more examples on your own! See, if you can come up with any surprising result.
If you haven't found any surprising result, it's because you haven't tried many examples. For example, try 7/3. Can you make sense of the result? Try also 1/2.
Python recognizes different types of numbers. The simplest type are the integers (or whole numbers). When Python divides an integer by another integer, it throws away any remainder to give us a whole number (integer) as the answer. Thus, when we divide 7 by 3 it gives us 2 (with a remainder of 1). To get the remainder part, we use the % symbol:
>>> 7/3 2 >>> 7%3 1 >>> 1/2 0 >>> 1%2 1
To get the result we would normally expect, we need to tell Python to use real numbers or floats. We do that by adding a decimal period ("dot") at the end of at least one of the numbers.
>>> 1./2 0.5 >>> 1/2. 0.5 >>> 1.00000/2 0.5
Python knows more than the basic mathematical operations. Here are a few more examples for you to try to expand on.
>>> 3*3*3*3 81 >>> 3**4 # exponentiation 81 >>> 7.3 % 3 # remainder, again 1.2999999999999998
This last result is almost equal to 1.3 which is what we might have expected. The difference between 1.3 and 1.2999999999999998 is tiny ... and is caused by the way computers work with decimal fractions. I will explain how this comes about in a later lesson, when you know more about computer programming in general. Just note that, in practice, such small difference between the "exact" result and that given by Python (or any other computer language) should not matter. Note however that Python can be made to display the result in a more sensible way; try the following:
>>> print 7.3 % 3
1.3
The print keyword instructs Python to show us the result of the calculation, and it does so "intelligently". Sometimes, Python will perform some computations without displaying the result. By using the print keyword, we can instruct Python to display a result that might not have been shown otherwise.
Are you curious? What happens if you put a print instruction in one of Reeborg's programs?...
Try the following:
>>> 2147483647 + 1 2147483648L
Look carefully: do you notice the curious "L" at the end of the answer?
This is to denote what is known as a Long integer, that is to say an
integer which can not be easily handled by the CPU. For a
computer with a so-called 32-bit chip, as an example, all positive numbers are represented by various combinations of 32
"bits", and the largest integer that can be thus represented is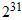 
-1 = 2147483647.
Any integer larger than this requires Python (or any other computer language)
to use advanced technique to perform mathematical operations on these
numbers. This slows down computations; Python reminds us of this by tagging
the letter L at the end. Unless you really need it, try to avoid using
extremely large numbers!
Try the following:
>>> 1,000 (1, 0) >>> 1,000,000,000 (1, 0, 0, 0)
What is going on? All I will say for now is that you should not put commas in numbers to separate thousands, like it is often done in many english-speaking coutries. We will see later what commas mean to Python. In the meantime, we can see what commmas mean when we put them in a print statement:
>>> print 5,4 5 4 >>> print 5, 4 5 4
Python takes the comma between the two numbers above to mean "put a single space between the two numbers (and ignore any other extra spaces) when you print them out.
You are perhaps familiar with the scientific notation:
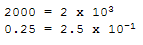
If so, you know that this notation allows us to write extremely small or extremely large numbers in a very convenient way. [If you don't know about the scientific notation, you can skip this section as we will not make use of it.] Python also knows the scientific notation but uses the letter E (or e) to represent x 10
>>> 2e3 2000.0 >>> 2.5E-1 0.25
Try it!
Python also knows how to manipulate complex numbers as well as octal (base 8) and hexadecimal (base 16) numbers. Do not worry if you don't know what these are. The only ones we will need to use are the hexadecimal numbers and we will explain what they are later.
Python knows how to compare numbers and decide if one is smaller than (<) the other, if it is greater than (>) the other, if they are equal (==) or if they are not equal (!=).
>>> 1<2 True >>> 3<2 False >>> 1>2 False >>> 3>2 True >>> 2==2 True >>> 3==2 False >>> 2!=2 False >>> 3!=2 True
Try it! Make sure to note the use of two equal signs when we want to check if two numbers are equal. If you use a single equal sign, Python will complain in its own way. [There are two other comparison operators: <=, >=. You can try them and guess what they might mean.]
Teaching Reeborg to add
