The failed addition at the end of the previous lesson surely came as a surprise to you. For the order of operands in an addition should not make any difference. But Python has to choose one and thus proceeds from left to right.
one = fraction(1) # Addition with a fraction coming first: one + 1 # The Python interpreter treats this as one.__add__(1)
And what if the fraction comes second? The integer 1 does not have any methods for fractions. Therefore Python tries to proceed from right to left by calling the method __radd__ of the object one:
# Addition with an integer coming first: 1 + one # The Python interpreter treats this as one.__radd__(1)
To fix the error you only have to define the method __radd__. And because the order of the operands must not influence the result __radd__ has to perform the same computation as __add__.
Python has floating point numbers (type float) after all! Each floating point number equals a fraction, e.g. 1.6 == 8/5 and 1.5 == 3/2. Floating point numbers seem to be more practical because one can see immediately that 1.6 is greater than 1.5 whereas with 8/5 and 3/2 you have to calculate a little to compare them. But fractions also have some good points. A floating point number equal to 1/3 would need to have a never ending sequence of 3 after the decimal point. But Computers usually do not store more than 15 digits (0.333333333333333) so that they have to make a tiny error if they try to represent 1/3 as a floating point number. Fractions on the other hand are exact. The Pythagoreans, a school of philosophers in the ancient Greece even believed that everything in the Universe could be traced back to proportions of integers, i.e. to fractions.
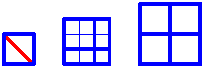
But soon this belief was shattered by doubts. Perhaps it all began with a bored Pythagorean who started to draw squares in the sand like these:

The squares show the connection between numbers and their square roots. The left square illustrates 1 * 1 == 1 therefore the square root of 1 is 1. The right square illustrates 2 * 2 == 4 therefore the square root of 4 is 2. The square in the middle shows that 3/2 * 3/2 == 9/4 (the subsquares with the thin borders are half as wide as the thick-bordered ones and thus have a quarter of their area). Thus 3/2 is the square root of 9/4 which is slightly greater than 2. Maybe this stimulated the Pythagorean's ambition to find the square root of 2. He knew that he had to search between 1 and 3/2 because 2 is between 1*1 and 3/2*3/2. So he started with 4/3 (too small) and 5/3 (too big) and went on to ever bigger numerators and denominators in order to approach and eventually find the square root of 2. The function find_square_root_of_2 below mimics the efforts of our Pythagorean:
def find_square_root_of_2(tries): '''Try to find the fraction num/denom which is the square root of 2: num/denom * num/denom == 2. ''' num = 0; denom = 1; error = 2 for t in range(tries): # Increase num until num/denom * num/denom is greater # or equal 2. while error > 0: num += 1 error = 2 * denom * denom - num * num # error 0 means num/denom is the square root of 2. if error == 0: return num, denom # Increase denom until num/denom * num/denom is less or # equal 2. while error < 0: denom += 1 error = 2 * denom * denom - num * num # error 0 means num/denom is the square root of 2. if error == 0: return num, denom # Return num, denom and num/denom * num/denom as a # floating point number. return num, denom, 1.0*num*num/denom/denom
Save find_square_root_of_2 and execute it with 10, 100 and 1000 tries. You can try even bigger numbers if you are patient enough. Can you find anything remarkable when comparing the results?
Our Pythagorean for sure didn't try as much as you did -- after all he didn't have Python and had to calculate everything in his head. But at some point a wicked suspicion must have bubbled up. Does the square root of 2 not exist at all? But no, the length of the red diagonal in the small square above with side length 1 is exactly square root of 2. So the square root of 2 is perhaps not a fraction at all?
To prove this conjecture you can not simply go on with calculating. For calculation never stops if the conjecture holds. We need a proof! Let us start with two assumptions:
simplify from the fraction lessons
and announce 4/3 as the result. A consequence of this rule is that at least
one of the numbers n and d can be made odd.
Now let us play a little with assumption 1. If n/d is the square root of 2, then n/d * n/d == 2 or n * n == 2 * d * d. Thus n * n is an even number. But then n must also be even. This means that n * n is a multiple of 4. Then finally d * d must also be even and by the same argument d! Thus from assumption 1 follows that n and d MUST BOTH be even numbers. This is a contradiction to assumption 2 which is true by the very nature of fractions. Two even numbers can be divided by 2 until at least one of them is odd - without changing the value of the fraction. The conclusion is bitter for the Pythagoreans:
ASSUMPTION 1 IS WRONG. THE SQUARE ROOT OF 2 IS NOT A FRACTION.
Computer programs are a valuable help for performing complex and tedious calculations. Some problems however cannot be solved by computer programs - like the problem of the Pythagorean. It is therefore not sufficient to know how to write programs. Intuition, logic and knowledge (mathematical knowledge in our case) are at least equally important. At this point I would like to thank you for your curiosity and patience which let you come this far. Good luck for your learning and work!