11.6 Putting it into Prolog

It is not particularly difficult to write a Prolog program that carries out bottom-up active chart parsing. Indeed, the code is probably slightly simpler than the code for the passive chart parser that we studied in the last chapter.

But before we get into it, let's briefly review the built in predicate findall/3 as we are going to make extensive use of it. findall is a predicate for finding all solutions to a goal or a sequence of goals. Queries of the form

findall(+Object, +Goal, -List)

compute a list of all instantiations of Object that satisfy Goal. The query

?- findall(X, happy(X), L).

for example, would give you a list of all instantiations of X such that happy(X) is satisfied. Object doesn't necessarily have to be a variable. For example,

?- findall(happy_duck(X), (happy(X), duck(X)), L).

would give you a list with all instantiations of happy_duck(X) such that happy(X), duck(X) is satisfied. So, assuming that your database looks as follows

duck(tick). duck(trick). duck(track). duck(dagobert). happy(tick). happy(trick). happy(track).

Prolog would answer

L = [happy_duck(tick), happy_duck(trick), happy_duck(track)]

Now, let's look at the implementation of the parser. First, we have to decide how to represent arcs. We are going to use the same strategy as in the last chapter and use a predicate, which we call arc for that. In addition to the positions that the arc spans, this predicate has to encode a dotted rule. We will therefore use arc with five arguments in the following way:

arc(Start, End, LHS, FoundSoFar, ToFind)

The three last arguments represent the information contained in the `.' notation of rules. LHS is the left hand side, FoundSoFar is the list of those symbols that are to the left of the dot, and ToFind are those that are to the right of the dot. For example, the arc

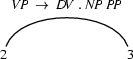
is represented as

arc(2, 3, vp, [dv], [np, pp])

One important thing to notice is that we represent the categories in FoundSoFar in reversed order. So

would be

arc(2, 5, vp, [np, dv], [pp]).

For representing the chart, we will again use the Prolog database. The agenda will be represented as a list. New edges are added by just appending them to the front (or the end).

The main predicate is active_chart_recognize/1. It takes a list of words (the input sentence) as argument and succeeds if we can:

Initialize the chart and agenda. (step 1 of the general algorithm)
Build the chart while processing the agenda until it's empty. (step 2)
End up with a chart containing a passive s arc that leads from the first node to the last node. (step 3)

Here is the code:

%%% active_chart_recognize(+sentence) active_chart_recognize(Input) :- cleanup, %%% step 1 initialize_chart_bottomup(Input, 0), initialize_agenda_bottomup(Agenda), %%% step 2 process_agenda(Agenda), %%% step 3 length(Input, N), arc(0, N, s, _, []).

Now, let's look at the initialization predicates. We said that the initial chart is exactly as for the passive chart parser. So, initialize_chart_bottomup/2 looks exactly like the initialze_chart/2 predicate of the last chapter:

%%% initialize_chart_bottomup(+sentence, +start node) initialize_chart_bottomup([], _). initialize_chart_bottomup([Word|Input], From) :- To is From + 1, assertz(scan(From, To, Word)), initialize_chart_bottomup(Input, To).

The initial agenda should contain passive arcs recording the position and category of the words of the input sentence. We retrieve one word and its category using the following sequence of goals

scan(From, To Word), lex(Word, Cat).

To get all categories for all of the words, we simply use findall. The passive arc is constructed directly in the first argument of findall.

%%% initialize_agenda_bottomup(-agenda) initialize_agenda_bottomup(Agenda) :- findall(arc(From, To, Cat, [Word], []), ( scan(From, To, Word), lex(Word, Cat) ), Agenda ).

This is what we need to carry out step 1 of the general algorithm in a bottom-up fashion. Now, let's look at step 2, the loop which does most of the work.

process_agenda/1 is a recursive predicate. Its argument is the list representing the agenda. It takes the first arc off that list and processes it. This may add new arguments to the agenda. In the end it recursively calls itself with the new agenda as argument. The recursion stops when the agenda is empty.

Processing of an arc works as follows. We make sure that the arc is not in the chart, yet, and add it. (That's step 2b of the general algorithm.) Predicate make_new_arcs_bottomup/2 then carries out steps 2c and 2d which may create new arcs. These are appended to the front of the agenda. If the arc is already in the chart, we throw it away and look at the rest of the agenda.

%%% process_agenda(+agenda) process_agenda([]). process_agenda([Arc|Agenda]) :- \+ Arc,!, assert(Arc), make_new_arcs_bottomup(Arc, NewArcs), append(NewArcs, Agenda, NewAgenda), process_agenda(NewAgenda). process_agenda([_|Agenda]) :- process_agenda(Agenda).

There are two steps in the general algorithm which generate new rules: steps 2c and 2d. In the bottom-up case, step 2c is applied to all edges, while step 2d is applied only to passive edges. The predicate make_new_arcs_bottomup/2 therefore has two clauses which carry out only step 2c (apply_fundamental_rule/2) or step 2c and step 2d (predict_new_arcs_bottomup/2) depending on whether the arc that's coming in is active or passive.

%%% make_new_arcs_bottomup(+arc, -list of arcs) %%% 'arc' is active -> only step 2c applies. make_new_arcs_bottomup(Arc, NewArcs) :- apply_fundamental_rule(Arc, NewArcs). %%% 'arc' is passive -> steps 2c and 2d apply make_new_arcs_bottomup(Arc), NewArcs) :- apply_fundamental_rule(Arc, NewArcs1), predict_new_arcs_bottomup(Arc, NewArcs2), append(NewArcs1, NewArcs2, NewArcs).

apply_fundamental_rule/2 tries to apply the fundamental rule to the arc given in the first argument. There are two clauses: one for those cases where we are dealing with a passive arc and one for those cases where we are dealing with an active arc. In the first case, we have look for an active arc which satisfies the following two conditions:

The active arc ends in the starting position of the passive arc.
The next category that the active arc has to find is what the passive arc has on its left hand side.

We again use findall to collect all possible solutions.

%%% apply_fundamental_rule(+arc, -list of arcs) apply_fundamental_rule(arc(J, K, Cat, _, []), NewArcs) :- findall(arc(I, K, SuperCat, [Cat|Done], Cats), arc(I, J, SuperCat, Done, [Cat|Cats]), NewArcs ).

In case we are dealing with an active arc, we looking for a passive arc in the chart.

apply_fundamental_rule(arc(I, J, Cat, Done, [SubCat|SubCats]), NewArcs) :- findall(arc(I, K, Cat, [SubCat|Done], SubCats), arc(J, K, SubCat, _, []), NewArcs ).

When processing the chart in a bottom-up fashion we only apply step 2d to passive rules. In that case, we look for grammar rules that have the left hand side of the arc as the first symbol in the right hand side. findall again gives us all possible solutions.

%%% predict_new_arcs_bottomup(+arc, -list of arcs) predict_new_arcs_bottomup(arc(J, _, Cat, _, []), NewArcs) :- findall(arc(J, J, SuperCat, [], [Cat|Cats]), SuperCat ---> [Cat|Cats], NewArcs ).

You can find the whole code in active_chart_bottomup.pl.