5 RTN transducers and ATNs
This lecture has two main goals:
To show that we can use RTNs as transducers, and to implement (again by extending our earlier work) a Prolog program that carries out RTN-based transduction.
To discuss Augmented Transition Networks (ATNs), a historically important way of extending RTNs that is no longer widely used. Understanding the shortcomings of ATNs will help motivate our later work on grammars and features.
5.1 Using RTNs as transducers
As we have discussed, FSAs can be adapted to work on two or more tapes, thereby becoming FSTs. So it shouldn't come as much of a surprise to learn that RTNs can also be used to transduce between two or more tapes, thereby becoming RTN transducers (or pushdown transducers). I'll briefly introduce the idea by examples, using Prolog notation, and then I'll note how we can adapt our previous code to work with such networks.
5.1.1 Two examples
Let's begin with a simple example. Recall that our first example of an RTN last week was rtnEng1.pl, a simple RTN that with three subnetworks, that produced simple sentences such as ``a wizard flies a broomstick''. It's easy to turn this into a transducer which systematically replaces all male words by female ones. Actually, as far as the definitions of the subnetworks is concerned, no changes need to be made:
%%%%%%%%%%%%%%%%%%
% The s subnetwork
%%%%%%%%%%%%%%%%%%
initial(0,s).
final(2,s).
arc(0,1,np,s).
arc(1,2,vp,s).
%%%%%%%%%%%%%%%%%%%
% The np subnetwork
%%%%%%%%%%%%%%%%%%%
initial(0,np).
final(2,np).
arc(0,1,det,np).
arc(1,2,n,np).
%%%%%%%%%%%%%%%%%%%
% The vp subnetwork
%%%%%%%%%%%%%%%%%%%
initial(0,vp).
final(2,vp).
arc(0,1,v,vp).
arc(1,2,np,vp).All the changes occur in the lexicon. Once again, we indicate that two strings can be transduced by using a list of length two:
word(n,[wizard,witch]).
word(n,[broomstick,broomstick]).
word(np,['Harry','Hermione']).
word(np,['Voldemort','Petunia']).
word(det,[a,a]).
word(det,[the,the]).
word(v,[flies,flies]).
word(v,[curses,curses]).It should be clear that this network allows us to transduce between ``a wizard curses Harry'' and ``a witch curses Hermione''.
Let's have a look a a slightly more complex example, a simple French/English transducer. There are three subnetworks:
%%%%%%%%%%%%%%%%%%
% The s subnetwork
%%%%%%%%%%%%%%%%%%
initial(0,s).
final(2,s).
arc(0,1,np,s).
arc(1,2,vp,s).
%%%%%%%%%%%%%%%%%%%
% The np subnetwork
%%%%%%%%%%%%%%%%%%%
initial(0,np).
final(2,np).
arc(0,1,detFem,np).
arc(1,2,nFem,np).
arc(0,4,detMasc,np).
arc(4,2,nMasc,np).
arc(2,3,wh,np).
arc(3,2,vp,np).
%%%%%%%%%%%%%%%%%%%
% The vp subnetwork
%%%%%%%%%%%%%%%%%%%
initial(0,vp).
final(1,vp).
final(2,vp).
arc(0,1,v,vp).
arc(1,2,np,vp).
arc(1,3,[that,que],vp).
arc(3,2,s,vp).As lexicon we have:
word(nFem,[house,maison]).
word(nFem,[table,table]).
word(nMasc,[man,homme]).
word(nMasc,[horse,cheval]).
word(np,[john,jean]).
word(np,[mary,marie]).
word(np,[jean,jeanne]).
word(detFem,[the,la]).
word(detFem,[a,une]).
word(detFem,[this,cet]).
word(detMasc,[the,le]).
word(detMasc,[a,un]).
word(detMasc,[this,cette]).
word(v,[sees,voit]).
word(v,[hits,frappe]).
word(v,[sings,chante]).
word(v,[lacks,manque]).
word(wh,[who,qui]).
word(wh,[which,qui]).
word(wh,[that,qui]).For example, this lets us transduce ``John sees the house'' and ``Jean voit la maison''.
5.1.2 Handling RTN transducers in Prolog
This is a routine extension of previous work, so I'll only sketch the basic points. Once again, the main predicate is transduce, but this time it has six arguments.
transduce(Subnet,Node,String1,Rest2,String2,Rest2)Subnet is the name of the subnetwork being traversed. Node is the name of a state in that subnetwork. String1 and Rest2 are a difference list representation of the left-hand-side tape contents. String2 and Rest2 are a difference list representation of the right-hand-side tape contents.
transduce(Subnet,Node,X1,X1,X2,X2) :-
final(Node,Subnet).
transduce(Subnet,Node_1,X1,Z1,X2,Z2) :-
arc(Node_1,Node_2,Label,Subnet),
traverse(Label,X1,Y1,X2,Y2),
transduce(Subnet,Node_2,Y1,Z1,Y2,Z2).The predicate that does all the work is, once again, traverse/5. But here there is an important change: traverse/5 and transduce/6 are now mutually recursive. That is, not only does transduce/6 call traverse/5 (which is what happened in the finite state case) but traverse/5 also calls transduce/6. It is this mutual recursion which enables the subnetworks to call on each other.
traverse([Sym1,Sym2],[Sym1|Symbols1],Symbols1,
[Sym2|Symbols2],Symbols2) :-
\+(special(Sym1)),
\+(special(Sym2)).
traverse(Category,String_1,Rest_1,String_2,Rest_2) :-
word(Category,Word_pair),
traverse(Word_pair,String_1,Rest_1,String_2,Rest_2).
traverse(['#',S2],String1,String1,[S2|X2],X2).
traverse([S1,'#'],[S1|X1],X1,String2,String2).
traverse('#',String1,String1,String2,String2).
traverse(Subnet,String1,Rest1,String_2,Rest_2) :-
initial(Node,Subnet),
transduce(Subnet,Node,String1,Rest1,String_2,Rest_2). The definition of special1/ is the one used last week: that is, we treat the names of subnetworks as special symbols.
special('#').
special(Category) :- word(Category,_).
special(Subnet) :- initial(_,Subnet).It is easy to adapt our collection of driver predicates for working with this.
5.2 Augmented Transition Networks (ATNs)
In this section we will discuss ATNs, a historically important tool in computational linguistics. In the 1970s they were probably the most widely used tool for analyzing syntactic structure, but with the emergence of more declarative methods in the 1980s they gradually fell into disuse. However it is useful to know what ATNs are, if only because they remain one of the clearest examples of a procedural approach to computational linguistics. Understanding the shortcomings of ATNs will help you appreciate the declarative, ``grammar+feature''-based methods we shall discuss in subsequent lectures.
ATNs are extension of RTNs. That is, ATNs offer everything that RTNs do (in particular, named subnetworks and recursive calling of subnetworks) plus other computational possibilities. But before going any further, it's worth knowing that there isn't a precise definition of what an ATN is. This is in sharp contrast to both FSAs and RTNs: both these formalisms are precisely defined, and we know exactly what both these formalisms can and cannot do. ATNs, however, are basically RTNs augmented in certain `useful' ways, and different computational linguists have introduced different augmentations. However, some augmentations of RTNs are more or less standard, and in this section we shall look at two of these: the use of registers and the use of tests. This will give the reader the basic flavor of what syntactic processing using ATNs is like.
5.2.1 A first ATN: adding registers
ATNs are an extension of RTNs --- so the first question to ask is: why did computational linguists ever feel the need to add new computational resources to RTNs? Let's consider the matter.
Suppose that we want to transduce English noun phrases to French noun phrases. Now, in French, (most) adjectives come after the noun, whereas in English adjectives (mostly) come before the noun. For example, the French noun phrases ``un nom court'' translates to the English noun phrase ``a short name''. How can we write an RTN transducer to handle this? In fact, it's hard to do much better than the following:
short_# N_Masc #_court
1 - - - - - - -> 1a - - - -> 1b - - - - - -> 2
| |
| |
| |
green_# N_Masc #_vert
- - - - - - -> 2a - - - ->2b - - - - - ->
| |
| |
| |
red_# N_Masc #_rouge
- - - - - - -> 3a - - - ->3b - - - - - ->
| |
| |
| |
- - - - - - -> 4a - - - ->4b - - - - - ->
. .
. .
. .
. .
. .This is not a nice solution. For a start, we have to exhaustively list lots of adjectives. This is not only a lot of work, it suggests that RTNs are representationally inadequate. That is, the obvious generalization about French and English --- namely that in French, adjectives come after the noun, whereas in English they come before --- isn't reflected in a simple way. That is, instead of a nice simple explicit generalization, we just have a (very) long list of translations in which this fact is left implicit. Moreover, note that the above network doesn't really solve the problem completely anyway: it only works for nouns preceded by one adjective. And to make this kind of solution work for sequences of adjectives, it seems we will have to list all possible adjective sequences and their translation. This is unattractive and impossible to carry out completely, as there are infinitely many such sequences. What we'd really like is to list in the lexicon, once and for all that ``short'' translates to ``court'' and work with a formalism that can make use of this basic fact in any syntactic context whatsoever.
This problem leads us directly to what is probably the most common augmentation of RTNs: the use of registers. Basically, a register is a piece of memory designed to hold a particular kind of information. (If you are used to imperative programming languages such as C or Pascal, think of a register as a local variable.) Registers can (and have been) used for just about everything, and there is a fairly clear intuition that they can help us out here. The basic idea is that we will carry out translation by writing down translations of the various words in the appropriate register, and then putting the translation together when we leave the subnetwork. Here's an example: an ATN which does exactly this:
------------------------------------------------------------------
NP | | FDet | FAdjs | FNoun | FNP |
------------------------------------------------------------------
|
Det Noun |
-> 0 ----------------> 1 -------------------> 2 ------> |
FDet ::= fren(*) FNoun ::= fren(*) FNP ::= |
/ \ FDet + |
/ \ FNoun + |
Adj /\ FAdjs |
\ / |
\ / |
- |
FAdjs ::= FAdjs + fren(*) |
------------------------------------------------------------------There are two important things to notice about this diagram. The first is the registers: these are the four
|
boxes at the top right hand side. Second, note that each transition arrow is labelled in a more complicated way. For example, the Det transition from 0 to 1 is labelled by
|
(This may remind you of an assignment statement in an imperative programming language --- and, indeed, that's pretty much what it is.)
The best way to understand all this new notation is to put it to work. Consider what happens when we are scanning the ``a'' in the string ``a short name'', and we enter the NP network.
We enter the NP network at its initial state 0. All four registers are initialized to contain the empty string.
We can get from O to 1 if we are scanning a determiner. But (as the lexicon presumably tells us), ``a'' is determiner, so we go into state 1 and are now scanning ``short''. But just as important --- indeed, more important --- is the side effect caused by the instruction
FDet ::= fren(*)that is associated with this transition. This means: take the French translation of the word you consumed while making the transition, and put the result in the
FDetregister. Now, the word consumed while making this transition was ``a'', and the French translation of this is ``un'' (let's assume that we are only dealing with masculine nouns) so as a side effect we have thatFDetnow contains ``un''.We can loop from 1 back to 1 if we are scanning an adjective. But (as the lexicon should tell us), ``short'' is an adjective, so we go back into state 1 and are now scanning ``name''. But, once again, it's the side effect associated with this transition that's important. The instruction
FAdjs ::= FAdjs + fren(*)means: take the French translation of the word you consumed while making this transition, and put the result at the end of the
FAdjsregister. The word we consumed while making this transition was ``short'', and the French translation of this is ``court'' (once again we assume that we are only dealing with masculine nouns) so as a side effect we have thatFAdjscontains ``court''. One remark: this side effect is not intended to overwrite what is already in the register --- the idea is to add the translation to the end of what's already there. In this example, this doesn't make a difference, for the register contained the empty string when we added ``court''. But if we had a whole sequence of adjectives to translate, we'd just keep looping from state 1 to state 1, translating all the adjectives one by one, and adding them one at a time to theFAdjsregister. Because we add all these new translations without overwriting, eventuallyFAdjswould contain a whole sequence of French adjectives, in the right order.We can go from 1 to 2 if we are scanning a noun. But ``name'' is an noun, so we go into state 2. We have now scanned all the symbols in the input. The side effect caused by the instruction
FNoun ::= fren(*)is: take the French translation of the word you consumed while making this transition, and put the result in the
FNounregister. The word we consumed while making this transition was ``name'', its French translation is ``nom'', soFNounnow contains ``nom''.We are in the final state and are ready to leave the NP subnetwork. But there is a side effect associated with leaving the subnetwork, namely
FNP ::= FDet + FNoun + FAdjs/That is, the register
FNPis loaded with the words inFDet,FNoun, andFAdjs, in that order. SoFNPwill be loaded with ``a nom court''. And that's the translation we want. So we are using theFNPto pass the correct answer back to whichever subnetwork called the NP subnetwork.
5.2.2 A second ATN: adding tests
Once we have the idea of adding registers to RTNs, another idea naturally suggests itself: why not add the ability to test the contents of registers, and carry out various acts depending on the results of such test?
Here's a second ATN, a modification of the previous one, which makes use of this idea:
------------------------------------------------------------------
NP | | Gender | FDet | FAdjs | FNoun | FNP |
------------------------------------------------------------------
FGender ::= fem
FDet ::= fren(*,fem)
------>---- ----->----
/ Det \ / Adj \
/ \ / \ FAdj ::= FAdjs +
/ \ / \ fren(*,Gender)
/ \ / \
-> 0 1 --------<----------
\ / \
\ / \
\ / \
\ Det / \
----->---- \
FGender ::= masc \
FDet ::= fren(*,masc) \
\ Noun
\
-------->---------- 2 ---------->
FNoun ::= fren(*) FNP ::=
? Gender = gender(FNoun) FDet +
FNoun +
FAdj
------------------------------------------------------------------ The main differences between this ATN and the previous one are (a) there is an additional register, called Gender, (b) there are now two Det arcs between 0 and 1, one which handles masculine determiners, the other feminine, (c) the fren construct now takes two arguments, not one, and (d) on the Noun arc between 1 and 2 we have the following test
? Gender = gender(FNoun). So what does this ATN do? Basically, this one can handle both masculine and feminine nouns. Let's see how it does this by considering what happens when we are scanning the ``a'' in the string ``a short name'', and we enter this NP subnetwork.
We enter the NP network at its initial state 0. The five registers are initialized to contain the empty string.
We can get from O to 1 if we are scanning a determiner --- indeed, two different transitions let us do this. Suppose we choose the top transition. Actually, this is the wrong choice, as ``name'' translates into ``nom'', which is masculine. But it's more interesting to make this wrong choice, for we'll later see how the test forces the ATN to backtrack to make the right one. The side effect associated with the top Det transition has two parts:
FGender ::= fem
FDet ::= fren(*,fem)The first part means: set the value if the
Genderregister tofem, signalling that we are (wrongly!) expecting a feminine noun. The second part means: take the French translation of the word you consumed while making the transition, translate it as feminine, and put the result in theFDetregister. Now, the word consumed while making this transition was ``a'', and the French translation of this as a feminine determiner is ``une''. SoFDetnow contains ``une''.We can loop from 1 back to 1 if we are scanning an adjective, and ``short'' is an adjective, so we go back into state 1 and are now scanning ``name''. What about the side effect? The instruction
FAdjs ::= FAdjs + fren(*,Gender)means: take the French translation of the word you consumed while making this transition, translate it with the gender stored in the
Genderregister, and put the result at the end of theFAdjsregister. The word we consumed while making this transition was ``short'',Gendercontainsfem, and the feminine French translation of short is ``courte'', so nowFAdjscontains ``courte''.We can go from 1 to 2 if we are scanning a noun. But ``name'' is an noun, so we go into state 2. We have scanned all the symbols in the input. What about the side effect? We have two instructions:
FNoun ::= fren(*)
? Gender = gender(FNoun)The first part tells us to take the French translation of the words consumed, and put the result in the
FNounregister. The word we consumed while making this transition was ``name'', its French translation is ``nom', soFNounnow contains ``nom''. Then comes the test? Gender = gender(FNoun). This means: check whether the value of theGenderregister (which, you will recall form Step~2, isfem) is the same as the gender of the noun inFNoun. ButFNouncontains ``nom'' which is masculine. And hence:The test FAILS!Because the test fails, we have to backtrack to the node where we set the value of the
Genderregister. Recall this was done when we made the transition from 0 to 1. So we backtrack all the way back to there, resetting all the registers to the empty string, and start scanning ``a'' again. And we try again...So this time we go from from O to 1 by taking the bottom transition (the right choice). The side effect associated with the top Det transition has two parts:
FGender ::= masc
FDet ::= fren(*,masc)The first part sets the value of the
Genderregister tomasc, signalling that we are expecting a masculine noun. The second part means: take the French translation of the word you consumed while making the transition, translate it as masculine, and put the result in theFDetregister. Now, the word consumed while making this transition was ``a'', and the French translation of this as a masculine determiner is ``un''. SoFDetnow contains ``un''.We can loop from 1 back to 1 if we are scanning an adjective, and ``short'' is an adjective, so we go back into state 1 and are now scanning ``name''. What about the side effect? The instruction
FAdjs ::= FAdjs + fren(*,Gender)means: take the French translation of the word you consumed while making this transition, translate it with the gender stored in the
Genderregister, and put the result at the end of theFAdjsregister. The word we consumed while making this transition was ``short'',Gendercontainsmasc, and the masculine French translation of short is ``court'', so nowFAdjscontains ``court''.We can go from 1 to 2 if we are scanning a noun. But ``name'' is an noun, so we go back into state 2, and we have scanned all the symbols in the input. Again, for the side effect we have two instructions:
FNoun ::= fren(*)
? Gender = gender(FNoun)The first part tells us to take the French translation of the words consumed, and put the result in the
FNounregister --- so ``nom' is put inFNoun. Now for the crucial test? Gender = gender(FNoun). Is the value of theGenderregister the same as the gender of the noun inFNoun. Yes:Gendercontainmasc, andFNouncontains ``nom'' which is masculine. So :The test SUCCEEDS!We are now in the final state and are ready to leave the NP subnetwork. There is a side effect associated with leaving the subnetwork, namely
FNP ::= FDet + FNoun + FAdjsThat is, the register
FNPis loaded with the words inFDet,FNoun, andFAdjs, in that order. SoFNPwill be loaded with ``a nom court'', the translation we want.
5.2.3 Shortcomings of ATNS
Before criticizing ATNs, let's first consider their good points.
First, in their day, ATNs were successful, and large and impressive systems were built using them (in fact, for many years the ATN underlying the LUNAR system was probably the largest natural language processing system in the world). Secondly, at the time, ATNs did not merely seem a useful practical tool, they seemed theoretically motivated as well. The 1970s were the heyday of Chomsky's Transformational Grammar (before Transformational Grammar turned into Government and Binding theory, and then Minimalism). Transformational Grammar was based on the idea that natural languages had a so-called deep structure (which was generated by a context free grammar) and that the surface forms of the language were then produced by transformations which manipulated these base forms in various ways. If this is the model of language you feel is correct, ATNs look plausible as a processing mechanism. Roughly speaking, the underlying RTN can be viewed as dealing with the base grammar, and the writing and testing of registers (and we have only scratched at the surface of what was done with registers and tests) can be seen as a way of dealing with the transformations (so to speak, they allow us to `undo' the transformations).
So ATNs --- at least in their day --- were not only useful, they were intellectually respectable. Nowadays, however, we are much less happy with them. Why? For the following reasons:
ATNs don't really have much to do with natural language. Basically, they are an all purpose programming tool. Once you start inventing formalisms that allow you to write to registers, and to test registers and act on the result, you have basically invented some sort of general purpose programming language. And when you get right down to it, that's what ATNs are. If it's possible to compute something, you can dream up an ATN to compute it.
When we worked with FSAs and RTNs, we saw that we could neatly factor out the declarative knowledge in such networks from the processing ideas. That is, it was easy to treat both FSAs and RTNs as passive data structures that encoded syntactical information, and to extract this information by various kinds of general program (such as recognizers and parsers). Pretty clearly, we can't do this with ATNs. In both examples we saw today, declarative and procedural ideas are completely tangled together: it's hard to see how we can pull them apart. The practical drawback of this is that its hard to maintain and extend ATNs. The theoretical drawback is that ATNs don't permit a neat distinction between grammatical knowledge, and how that knowledge is used.
It's also worth noting that ATNs come close to killing the underlying idea of networks. In FSAs and RTNs, the idea of moving through a network, or calling other networks, is the idea that does all the work. But consider today's ATNs. At best, the moves through the network play a bookkeeping role. The real action is carried out by the writing to and testing of registers. That is, the sorts of augmentation we have seen today come close to eating the underlying RTN formalism alive.
For these reasons, we will not attempt to implement ATNs in Prolog. This could be done --- but the ATNs intrinsically procedural perspective is so at odds with Prolog's declarative ideology that it would be a pretty weird (not to mention, pointless) thing to do.
5.3 Concluding remarks
ATNs, then, aren't what we want for syntactic analysis. But this leaves us with a problem: the drawbacks of network based approaches to syntax that we noted above are real, and won't go away.
To solve these problems, we're going to drop the network idea altogether. As we've already seen, networks are really at their most useful in their simplest form: FSAs and FSTs. For syntax --- that is, when there is lots of recursive structure that needs analyzing --- we shall turn to another idea: grammars. As we shall see, when the idea of grammars is linked to the idea of features, we have a combination which will let us solve the problems mentioned today, and many more besides.
5.4 Exercises
Answer ``true'' or ``false'' to the following questions:
ATNs can recognize any context-free language.
RTNs cannot recognize any non-context free language.
It is possible to write an RTN for the language
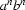 .
.It is possible to write an RTN for the language
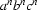 .
.It is possible to write an ATN for the language
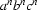 .
.RTNs are linguistically natural because they explicitly group information about particular syntactic categories (e.g. nouns and verbs) together in one place, rather than leaving it implicit and spread out.
RTNs are particularly useful in phonology and morphology.
ATNs are are widely used in modern computational linguistics.
Write an RTN for
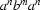 .
.Here is a Prolog/ description of an RTN:
initial(0,a). initial(3,c).
final(2,a). final(5,c).
arc(0,1,b,a). arc(3,4,f,c).
arc(1,2,c,a). arc(4,5,g,c).
initial(0,b). arc(0,1,d,b).
final(2,b). arc(1,2,e,b).Draw a picture of it.