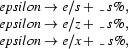3.3 Regular Languages and Relations

Towards the end of the last section, we saw that we luckily don't have to specify one (big) transducer that can deal with all spelling rules, but that it is enough to specify one (smaller) transducer per rule, because there are ways of combining these individual transducers into one big transducer. But still you might think that specifying the e-insertion transducer was actually quite tricky compared to formulating the rule that's behind it (``insert an e at a morpheme boundary, if it is preceded by s, x, or z, and followed by s and the end of the word). Now, there is way of formulating spelling rules that makes it possible to automatically translate them into transducers. And this is what we want to look at now.

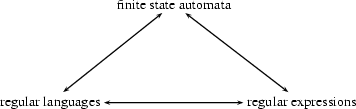
First, let's briefly go back to finite state automata. We said in Lecture 1 that the languages that FSA can recognize are called regular languages. But there is another way of defining regular languages: Regular languages are exactly those languages that can be represented by regular expressions. And from this it follows that every automaton corresponds to a regular expression and vice versa. So, we get the following picture:

But what are regular expressions? The building stones of regular expressions are symbols. These symbols can then be connected in a number of ways to represent sets of strings. We won't go into the details here (see the Further Reading Section if you want to know more) but just give a couple of examples. a and b are regular expressions representing the singleton sets of strings 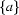$\{a\}$ and $\{b\}$ . 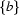They correspond to the following automata:

Regular expressions can be concatenated. The regular expression ab represents the (also singleton) set of strings 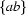$\{ab\}$ . It should be clear what the corresponding automaton looks like. We can furthermore combine regular expressions by disjunction. The regular expression a | (ab) represents the set of strings 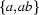$\{a, ab\}$ and corresponds to the automaton

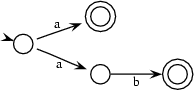
Finally, (a | b)* is the set of all strings that consist of as and bs in any order. The empty word is also accepted. The automaton looks as follows:

From the examples you might already have guessed that there is a systematic way of translating regular expressions into finite state automata, which means that we never actually have to specify automata -- we only have to write regular expressions.

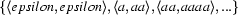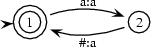
Now, let's go back to finite state transducers. Finite state transducers recognize tuples of strings. A set of tuples of strings that can be recognized by an FST is called a regular relation. So, regular relations are to FSTs what regular languages are to FSA. The following transducer (we have already seen it in the previous lecture), for instance, recognizes the regular relation $\{\langle epsilon,epsilon \rangle, \langle a,aa\rangle, \langle aa,aaaa\rangle, ...\}$ .

Regular relations can be specified using (ordered sets of) rewriting rules. The rewriting rules

$\begin{array}{l} epsilon \rightarrow e / s+\ \_\ s\%,\\ epsilon \rightarrow e / z+\ \_\ s\%,\\ epsilon \rightarrow e / x+\ \_\ s\%,\\ \end{array}$

for instance, express the e-insertion rule. The first one is read as ``replace nothing (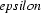 epsilon ) with e in the context of s+ (s and a morpheme boundary, +) to the left and s% (s and a word boundary, %) to the right. There are algorithms for translating such rule systems (at least, as long as they obey certain restrictions) into transducers.