2.6 Exercises
Answer ``true'' or ``false'' to the following questions:
It is possible to write a finite state automaton (FSA) to generate/recognize any formal language.
It is not possible to write an FSA that generates/recognizes the formal language
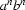 .
.It is not possible to write an FSA that generates/recognizes the formal language
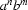 .
.Finite state methods are widely used in phonology and morphology.
We can generate more languages using non-deterministic finite automata than we can using deterministic finite automata.
A finite state transducer (FST) is essentially an FSA that works with 2 (or more) tapes.
It is useful to think of an FST as reading one of its tapes and writing to the other.
Write an FST that transduces between strings of as (of length
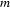 ), and strings consisting of a c, followed by
), and strings consisting of a c, followed by 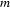 bs, followed by another c. For example, your FST should transduce between aaa and cbbbc. Write down your FST in both graphical and Prolog notation.
bs, followed by another c. For example, your FST should transduce between aaa and cbbbc. Write down your FST in both graphical and Prolog notation. Write an FST that, given a string of as, bs, and cs, deletes all the as, turns the bs to ds, and leaves the cs alone. For example, given the input abbaabcbca, your FST should transduce return dddcdc. Write down your FST in both graphical and Prolog notation.
Design an FST that transduces number names in written form between two languages you know (for all numbers from 0 to 100). For example, if you write a French_English FST, this should transduce between `ninety four' and `quatre vingt quatorze', and if you write a Dutch_German FST, this should transduce between `een en twintig' and `ein und zwanzig'.
In Lecture 1, we claimed that the formal language
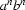 was relevant to natural language, because natural languages contain various ``balanced'' syntactic constructions. Give an example from some natural language you are familiar with (German, Irish, Russian, French, English, Japanese, Chinese, Tagalog,...). Make sure you explain why your answer is relevant.
was relevant to natural language, because natural languages contain various ``balanced'' syntactic constructions. Give an example from some natural language you are familiar with (German, Irish, Russian, French, English, Japanese, Chinese, Tagalog,...). Make sure you explain why your answer is relevant.