CSc 150
Final Exam Review Answers

  1. public int binSearch(int[] A, int key) {
   return binSearch(A, key, 0, A.length-1);
}

private int binSearch(int[] A, int key, int left, int right)
{
  int midpoint=(left+right)/2; // find midpoint of interval left:right
  if  (left > right)           // if the search interval is empty then
     return -1;             // return -1 to signal key not found
  else 
  {
     if (A[midpoint]==key)
        return midpoint;
     else if (key > A[midpoint]) 
        return binSearch(A, key, midpoint+1, right);
     else 
        return binSearch(A, key, left, midpoint-1);
  }   
}

  2. Here's one solution. Note the cast! 
    public void reverse()
{
   Queue q = new Queue();
   while (!this.isEmpty()) {
      q.insert(this.pop());
   }
   while (!q.isEmpty()) {
      this.push((String)q.remove());
   }
}
    It's also possible to write reverse without using a queue at all -- but just with the Stack class. Can you do it?

    1. Not a heap. Parent 44 is not bigger than child 77
    2. Heap.
    3. Heap.
    4. Not a heap. Heaps must be complete.
    5. Heap.
    6. Not a heap. Parent 22 is not bigger than child 55

  4. Here's one solution. Search until you find the node that points back to firstNode. And adjust that node's next pointer: 
    public void linearize()
{
   if (length > 0) {
      ListNode runner = firstNode;
      while (runner.next != firstNode) {
         runner = runner.next;
      }
      runner.next = null;
   }
}
    Note how this code handles both the 0-node and 1-node cases correctly.

  5. Here's one solution. Remember the two cases! The basic pseudocode is: 
    if the subtree rooted at N is an empty tree (base case)
   then return 0 (since the answer is 0 for an empty tree)
else {
   // it's the recursive case: a real node with two (possibly empty)
   // trees dangling off of it 
   if the real node is a leaf (which means N is the root of a 1-node tree)
      return 1 (since the answer is "1 leaf" for a 1-node tree)
   else  
      // real node that N points to is not a leaf, so the answer is
      // # of leaves in N's left subtree +
      // # of leaves in N's right subtree
      return (recursive call with N.llink) + (recursive call with N.rlink)
}
    Now just translate to code: 
    // returns number of leaves in tree
public int leafCount()
{
   return leafCount(root);
}
      
// # of leaves in the subtree rooted at N is equal to
// 0 if empty tree, 1 if N is a leaf, and if not a leaf,
// to the # of leaves in left subtree + # of leaves in right subtree
private int leafCount(BSTnode N)
{
   if (N == null)
     return 0;
   else if (N.llink==null && N.rlink==null)
     return 1;
   else return leafCount(N.llink) + leafCount(N.rlink);
}

  6. h(K) = K % 11
    p(K) = 1

    index: 0 1 2 3 4 5 6 7 8 9 10
    entry: 66 54           62 73 19 32

  7. h(K) = K % 11
    p(K) = max(1,(K/11)%11)

    index: 0 1 2 3 4 5 6 7 8 9 10
    entry: 66   73 54       62 19   32

  8.  

    This is the expression tree for a*((b+c)*(d*e+f)).

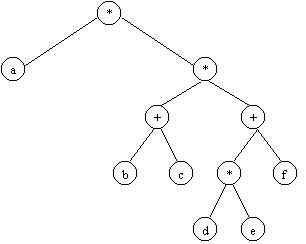
    This expression is different than the expression a*(b+c)*(d*e+f) because, without explicit parentheses, equivalent operations in infix expressions are assumed to be done in left-to-right order. Thus, the latter expression is equivalent to (a*(b+c))*(d*e+f) where we have explicitly stated that (b+c) should be multiplied by a first. The corresponding expression tree is:

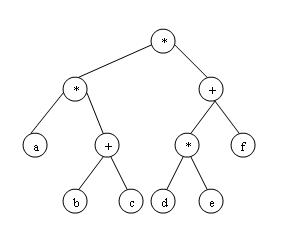
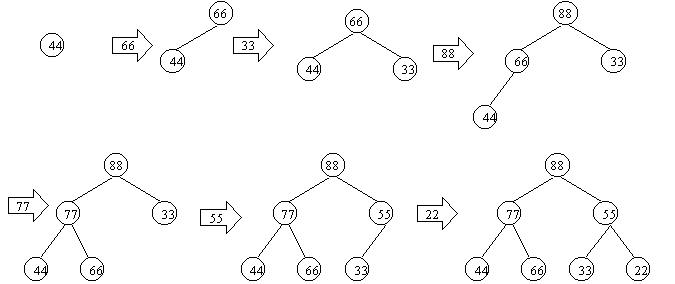
  9. Tree versions. Your trees should look EXACTLY the same.

    Array versions. Arrays start at index 1:

    Insert 44:

    44

    Insert 66:

    66 44

    Insert 33:

    66 44 33

    Insert 88:

    88 66 33 44

    Insert 77:

    88 77 33 44 66

    Insert 55:

    88 77 55 44 66 33

    Insert 22:

    88 77 55 44 66 33 22

CSc 150 homepage