Spreadsheets Lecture: Microsoft Excel

What are Spreadsheets?

• Like a large sheet of graph paper
• Used to store large tables of numbers and text
• Like an accountant's books

Main reasons to use a spreadsheet

Workbook Layout

A document in Excel is called a workbook.

• Like very large table (2D calculator)
• Columns labeled by letters
  • A-Z, AA-AZ, BA-BZ,...,IV = 256 columns
• Rows labeled by numbers
  • 1 to 16,384
• Cell = Intersection of row & column
• Cell Addresses (A1, B5, N34)
• Cell Contents
  • Text (Labels)
  • Numbers
  • Formulas
• Formula Bar
  • Reference Area a.k.a Name Box (Indicates current cell)
  • Cell contents area (Enter/Edit contents of a cell; shows a cell's true contents)
  • Cancel (X), Accept (checkmark), and Edit Formula Boxes
  • See the at-a-glance sheet for layout of the Formula bar and default toolbars.

Getting Help

• Bottom Left = mini help message
• Office Assistant

Entering Info

• Numbers
  • Use to enter "raw data" into a spreadsheet
  • Alter format via Cells... command in Format menu
    • format is cosmetic change only! (IMPORTANT)
    • change numbers into currency, percentage, date, time, etc.
• Text
  • Use for headings
  • Can change font, styles, alignment
  • Can use Toolbar to change
• Formulas
  • Used to do the bulk of the work in Excel
  • Cell names/addresses are variables
  • All formulas begin with "=" sign
  • Can do simple math (+, -, *, /)
  • Can type it in yourself or use the Function Wizard
• Using Pre-Selected region to enter info
  • Return key: down first
  • Enter key: right first
  • Control key: discontinuous selection

Editing Worksheets

• Adjusting rows and columns
  • Changing width/height
    • Use split bar between rows/cols
    • Use Autofit command under Format menu
  • Adjusting cell formats: use Cells... command in Format menu to:
    • change cell color
    • add a border to a cell
    • add a pattern
    • change font, size, style
  • Inserting/Deleting rows and columns
    1. Select row/column by clicking on column letter or row number
    2. Choose Delete from Edit menu or use Insert menu to add rows or columns
  • Selecting Cells/Areas
    • Use mouse to click and drag
    • Select entire spreadsheet by clicking on little blank space in upper-left (below formula bar)
    • In a formula, specify a range for a rectangular region of cells (top-left:bottom-right), eg. B6:C8 = B6,B7,B8,C6,C7,C8
• Cut
  • Used to MOVE info.
  • See help message
• Copy/Paste/Fill
  • Area to paste must be the same size as the copied area
  • Filling: Mass copy and paste; Access via Edit menu or by clicking and dragging when cursor is located in bottom-right corner of cell to be copied (cursor will be a solid black cross.)

Cell Addressing

• Relative
  • Default way of addressing
  • Cell addresses typed "normally": B3, A10, N8
  • Formulas change when copied/filled to another cell
  • Compare pictures below: before fill (left) & after fill (right)

  

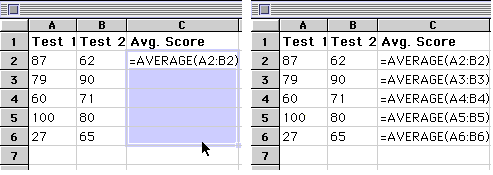
  Picture: On the left, you see a formula with 2 relative addresses: A2 and B2. A relative address will change when filled (copied & pasted), as shown by the changing formula on the right. In this case, we want the formula to change since we are finding different averages for each row of scores.

• Absolute
  • Cell addresses typed with dollar signs "locking" whatever follows them
  • Examples: $B$3 , $A$10 , $N$8
  • Always refer to same cell even after copy or fill
  • Compare pictures below: before fill (left) & after fill (right)

  

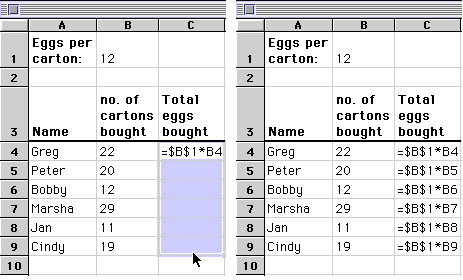
  Picture: The cell address $B$1 is an absolute address. This cell refers to the number of eggs per carton, 12, which never changes. It is used for every formula. By making it absolute, we prevent it from changing as the formula is filled downward. The cell B4 is left relative since we do wish it to change as the formula is pasted from row to row.

Printing

• Printing a selected area (using Page Setup in the File menu)
  • Sheet tab: setting a Print Area
  • Page tab: fit to a specified number of pages (you choose)
• Print Preview (File menu)
• Also using Page Setup in the File menu:
  • Add header/footer
  • Change orientation: portrait or landscape
  • Gridlines
  • Row and column headings
  • Adjust margins

Sorting

1. Select area to sort
2. Choose Sort from the Data menu
3. Select 1st key to sort on
4. Choose ascending (A-Z) or descending (Z-A) order

What-if? Scenarios

• Used to answer questions about possible future events
• "What do I need x to be in order to get y here?"
• Use Goal Seek under the Tools menu

Charts (Graphs)

• Using the Chart Wizard
  • Located in standard toolbar
  • Go through walkthrough to create chart
  • Can double click on any piece of the chart to edit it (title, axes, data, etc.)
• Once chart is opened (double-clicked on), you can access:
  • Chart menu
    • Chart Type - to change type of chart
    • Source Data - change which cells are being used to make chart. Also good for changing labels in legend
    • Chart Options
      • Titles (for titles of chart and axes)
      • Data Labels (to show values on graph itself)
      • Legend (do you want one?)
      • Axes (which should appear)
      • Gridlines (which should appear)
  • Click outside of chart in order to get out of Chart-Editing mode