8.1.3 Beyond context free languages

In the previous lecture we introduced DCGs as a useful Prolog tool for representing and working with context free grammars. Now, this is certainly a good way of thinking about DCGs, but it's not the whole story. For the fact of the matter is: DCGs can deal with a lot more than just context free languages. The extra arguments we have been discussing (and indeed, the extra tests we shall introduce shortly) give us the tools for coping with any computable language whatsoever. We shall illustrate this by presenting a simple DCG for the formal language 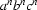a^nb^nc^n . %%-\{\epsilon\}/.

The formal language 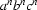a^nb^nc^n %%-\{\epsilon\}/ consists of all non-null strings made up of as, bs, and cs which consist of an unbroken block of as, followed by an unbroken block of bs, followed by an unbroken block of cs, all three blocks having the same length. For example, abc, and aabbcc and aaabbbccc all belong to 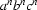a^nb^nc^n . %%-\{\epsilon\}/. Furthermore, $\epsilon$ belongs to .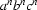

The interesting thing about this language is that it is not context free. Try whatever you like, you will not succeed in writing a context free grammar that generates precisely these strings. Proving this would take us too far afield, but the proof is not particularly difficult, and you can find it in many books on formal language theory.

On the other hand, as we shall now see, it is very easy to write a DCG that generates this language. Just as we did in the previous lecture, we shall represent strings as lists; for example, the string abc will be represented using the list [a,b,c]. Given this convention, here's the DCG we need:

s(Count) --> ablock(Count),bblock(Count),cblock(Count). ablock(0) --> []. ablock(succ(Count)) --> [a],ablock(Count). bblock(0) --> []. bblock(succ(Count)) --> [b],bblock(Count). cblock(0) --> []. cblock(succ(Count)) --> [c],cblock(Count).

The idea underlying this DCG is fairly simple: we use an extra argument to keep track of the length of the blocks. The s rule simply says that we want a block of as followed by a block of bs followed by block of cs, and all three blocks are to have the same length, namely Count.

But what should the values of Count be? The obvious answer is: 1, 2, 3, 4,..., and so on. But as yet we don't know how to mix DCGs and arithmetic, so this isn't very helpful. Fortunately there's an easier (and more elegant) way. Represent the number 0 by 0, the number 1 by succ(0), the number 2 by succ(succ(0)), the number 3 by succ(succ(succ(0))),..., and so on, just as we did it in Chapter 3. (You can read succ as ``successor of''.) Using this simple notation we can ``count using matching''.

This is precisely what the above DCG does, and it works very neatly. For example, suppose we pose the following query:

s(Count,L,[]).

which asks Prolog to generate the lists L of symbols that belong to this language, and to give the value of Count needed to produce each item. Then the first three responses are:

Count = 0 L = [] ; Count = succ(0) L = [a, b, c] ; Count = succ(succ(0)) L = [a, a, b, b, c, c] ; Count = succ(succ(succ(0))) L = [a, a, a, b, b, b, c, c, c]

The value of Count clearly corresponds to the length of the blocks.

So: DCGs are not just a tool for working with context free grammars. They are strictly more powerful than that, and (as we've just seen) part of the extra power comes from the use of extra arguments.