7.2.3 A DCG for a simple formal language

As our last example, we shall define a DCG for the formal language 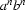a^nb^n . What is this language? And what is a formal language anyway?

A formal language is simply a set of strings. The term `formal language' is intended to contrast with the term `natural language': whereas natural languages are languages that human beings actually use, fomal languages are mathematical objects that computer scientists, logicians, and mathematicians define and study for various purpose.

A simple example of a formal language is 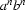a^nb^n . There are only two `words' in this language: the symbol a and the symbol b. The language 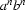a^nb^n consist of all strings made up from these two symbols that have the following form: the string must consist of an unbroken block of as of length n, followed by an unbroken block of bs of length n, and nothing else. So the strings ab, aabb, aaabbb and aaaabbbb all belong to 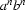a^nb^n . (Note that the empty string belongs to 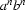a^nb^n too: after all, the empty string consists of a block of as of length zero followed by a block of bs of length zero.) On the other hand, aaabb and aaabbba do not belong to a^nb^n .

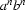Now, it is easy to write a context free grammar that generates this language:

s -> $\epsilon$

s -> l s r

l -> a

r -> b

The first rule says that an s can be realized as nothing at all. The second rule says that an s can be made up of an l (for left) element, followed by an s, followed by an r (for right) element. The last two rules say that l elements and r elements can be realized as as and bs respectively. It should be clear that this grammar really does generate all and only the elements of 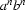a^nb^n , including the empty string.

Moreover, it is trivial to turn this grammar into DCG. We can do so as follows:

s --> []. s --> l,s,r. l --> [a]. r --> [b].

And this DCG works exactly as we would hope. For example, to the query

s([a,a,a,b,b,b],[]).

we get the answer `yes', while to the query

s([a,a,a,b,b,b,b],[]).

we get the answer `no'. And the query

s(X,[]).

enumerates the strings in the language, starting from [].