6.1.2 Using append

Now that we understand how append works, let's see how we can put it to work.

One important use of append is to split up a list into two consecutive lists. For example:

append(X,Y,[a,b,c,d]).
 
X = []  
Y = [a,b,c,d] ;
 
X = [a]  
Y = [b,c,d] ;
 
X = [a,b]  
Y = [c,d] ;
 
X = [a,b,c]  
Y = [d] ;
 
X = [a,b,c,d]  
Y = [] ;
 
no

That is, we give the list we want to split up (here[a,b,c,d]) to append as the third argument, and we use variables for the first two arguments. Prolog then searches for ways of instantiating the variables to two lists that concatenate to give the third argument, thus splitting up the list in two. Moreover, as this example shows, by backtracking, Prolog can find all possible ways of splitting up a list into two consecutive lists.

This ability means it is easy to define some useful predicates with append. Let's consider some examples. First, we can define a program which finds prefixes of lists. For example, the prefixes of [a,b,c,d] are [], [a], [a,b], [a,b,c], and [a,b,c,d]. With the help of append it is straightforward to define a program prefix/2, whose arguments are both lists, such that prefix(P,L) will hold when P is a prefix of L. Here's how:

prefix(P,L) :- append(P,_,L).

This says that list P is a prefix of list L when there is some list such that L is the result of concatenating P with that list. (We use the anonymous variable since we don't care what that other list is: we only care that there some such list or other.) This predicate successfully finds prefixes of lists, and moreover, via backtracking, finds them all:

prefix(X,[a,b,c,d]).
 
X = [] ;
 
X = [a] ;
 
X = [a,b] ;
 
X = [a,b,c] ;
 
X = [a,b,c,d] ;
 
no

In a similar fashion, we can define a program which finds suffixes of lists. For example, the suffixes of [a,b,c,d] are [], [d], [c,d], [b,c,d], and [a,b,c,d]. Again, using append it is easy to define suffix/2, a predicate whose arguments are both lists, such that suffix(S,L) will hold when S is a suffix of L:

suffix(S,L) :- append(_,S,L).

That is, list S is a suffix of list L if there is some list such that L is the result of concatenating that list with S. This predicate successfully finds suffixes of lists, and moreover, via backtracking, finds them all:

suffix(X,[a,b,c,d]).
 
X = [a,b,c,d] ;
 
X = [b,c,d] ;
 
X = [c,d] ;
 
X = [d] ;
 
X = [] ;
 
no

Make sure you understand why the results come out in this order.

And now it's very easy to define a program that finds sublists of lists. The sublists of [a,b,c,d] are [], [a], [b], [c], [d], [a,b], [b,c], [c,d], [d,e], [a,b,c], [b,c,d], and [a,b,c,d]. Now, a little thought reveals that the sublists of a list L are simply the prefixes of suffixes of L. Think about it pictorially:

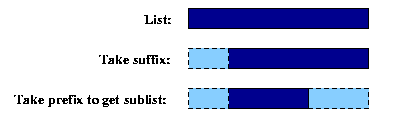
And of course, we have both the predicates we need to pin this ideas down: we simply define

sublist(SubL,L) :- suffix(S,L),prefix(SubL,S).

That is, SubL is a sublist of L if there is some suffix S of L of which SubL is a prefix. This program doesn't explicitly use append, but of course, under the surface, that's what's doing the work for us, as both prefix and suffix are defined using append.