3.1.1 Example 1: Eating

Consider the following knowledge base:

is_digesting(X,Y) :- just_ate(X,Y).
is_digesting(X,Y) :-  
        just_ate(X,Z),
        is_digesting(Z,Y).
 
just_ate(mosquito,blood(john)).
just_ate(frog,mosquito).
just_ate(stork,frog).

At first glance this seems pretty ordinary: it's just a knowledge base containing two facts and two rules. But the definition of the is_digesting/2 predicate is recursive. Note that is_digesting is (at least partially) defined in terms of itself, for the is_digesting functor occurs on both the left and right hand sides of the second rule. Crucially, however, there is an `escape' from this circularity. This is provided by the just_ate predicate, which occurs in both the first and second rules. (Significantly, the right hand side of the first rule makes no mention of is_digesting.) Let's now consider both the declarative and procedural meanings of this rule.

The word declarative is used to talk about the logical meaning of Prolog knowledge bases. That is, the declarative meaning of a Prolog knowledge base is simply `what it says', or `what it means, if we read it as a collection of logical statements'. And the declarative meaning of this recursive definition is fairly straightforward. The first clause (the `escape' clause, the one that is not recursive, or as we shall usually call it, the base clause), simply says that: if X has just eaten Y, then X is now digesting Y. This is obviously a sensible definition.

So what about the second clause, the recursive clause? This says that: if X has just eaten Z and Z is digesting Y, then X is digesting Y, too. Again, this is obviously a sensible definition.

So now we know what this recursive definition says, but what happens when we pose a query that actually needs to use this definition? That is, what does this definition actually do? To use the normal Prolog terminology, what is its procedural meaning?

This is also reasonably straightforward. The base rule is like all the earlier rules we've seen. That is, if we ask whether X is digesting Y, Prolog can use this rule to ask instead the question: has X just eaten Y?

What about the recursive clause? This gives Prolog another strategy for determining whether X is digesting Y: it can try to find some Z such that X has just eaten Z, and Z is digesting Y. That is, this rule lets Prolog break the task apart into two subtasks. Hopefully, doing so will eventually lead to simple problems which can be solved by simply looking up the answers in the knowledge base. The following picture sums up the situation:

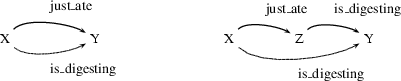
Let's see how this works. If we pose the query:

?- is_digesting(stork,mosquito). 

then Prolog goes to work as follows. First, it tries to make use of the first rule listed concerning is_digesting; that is, the base rule. This tells it that X is digesting Y if X just ate Y, By unifying X with stork and Y with mosquito it obtains the following goal:

just_ate(stork,mosquito). 

But the knowledge base doesn't contain the information that the stork just ate the mosquito, so this attempt fails. So Prolog next tries to make use of the second rule. By unifying X with stork and Y with mosquito it obtains the following goals:

just_ate(stork,Z),  
is_digesting(Z,mosquito).

That is, to show is_digesting(stork,mosquitp)}, Prolog needs to find a value for Z such that, firstly,

just_ate(stork,Z).

and secondly,

is_digesting(Z,mosquito).

And there is such a value for Z, namely frog. It is immediate that

just_ate(stork,frog).

will succeed, for this fact is listed in the knowledge base. And deducing

is_digesting(frog,mosquito).

is almost as simple, for the first clause of is_digesting/2 reduces this goal to deducing

just_ate(frog,mosquito).

and this is a fact listed in the knowledge base.

Well, that's our first example of a recursive rule definition. We're going to learn a lot more about them in the next few weeks, but one very practical remark should be made right away. Hopefully it's clear that when you write a recursive predicate, it should always have at least two clauses: a base clause (the clause that stops the recursion at some point), and one that contains the recursion. If you don't do this, Prolog can spiral off into an unending sequence of useless computations. For example, here's an extremely simple example of a recursive rule definition:

p :- p.

That's it. Nothing else. It's beautiful in its simplicity. And from a declarative perspective it's an extremely sensible (if rather boring) definition: it says `if property p holds, then property p holds'. You can't argue with that.

But from a procedural perspective, this is a wildly dangerous rule. In fact, we have here the ultimate in dangerous recursive rules: exactly the same thing on both sides, and no base clause to let us escape. For consider what happens when we pose the following query:

?- p.

Prolog asks itself: how do I prove p? And it realizes, `Hey, I've got a rule for that! To prove p I just need to prove p!'. So it asks itself (again): how do I prove p? And it realizes, `Hey, I've got a rule for that! To prove p I just need to prove p!'. So it asks itself (yet again): how do I prove p? And it realizes, `Hey, I've got a rule for that! To prove p I just need to prove p!'' So then it asks itself (for the fourth time): how do I prove p? And it realizes that...

If you make this query, Prolog won't answer you: it will head off, looping desperately away in an unending search. That is, it won't terminate, and you'll have to interrupt it. Of course, if you use trace, you can step through one step at a time, until you get sick of watching Prolog loop.