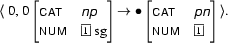14.2.1 The Fundamental Rule

The fundamental rule for feature structure based grammars says that an active arc and a passive arc can be combined if

1. the passive arc starts in the position where the active arc ends

2. the active arc is looking for a category 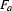which is unifiable with the category 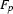that is provided by the passive arc.

The new arc starts in the starting position of the active arc and ends in the ending position of the passive arc. The label of the new arc is built as follows. We take the label of the active arc, we unify 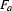with 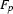and advance the dot by one position. Here are some examples.

The active arc

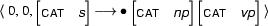
and the passive arc

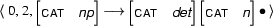
can be combined by applying the fundamental rule. Why? The active arc ends in 0 and that's where the passive arc starts. Furthermore,

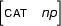
is unifiable with

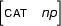
The resulting new arc is

Here is a more interesting example. The active arc as above, but let the passive arc be

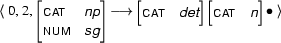
These two arc can also be combined: their starting and ending positions are compatible with the requirements of the rule and furthermore

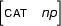
is unifiable with

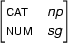
The result of this unification is

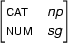
So, the new arc that is created looks like this:

In the last example, the application of the fundamental rule not only moved the dot, but also specified the active arc further. This mechanism together with co-indexation of values within a rule can lead to propagation of information to other parts of the rule. Let's see an example. Here are the active and the passive rule:

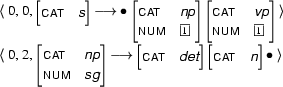
The result of combining them is

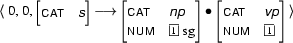
The new arc is looking for a vp. But because of the co-indexation it is not looking just for any vp but for a singular vp.

So, this is how the fundamental rule works. If you compare it to the fundamental rule for context free grammars, you will see we really just replaced identity of atomic categories by unification of feature structures. I.e., at all places where we said before that two categories have to be the same we now say that they have to unify.

14.2.2 Bottom-up Chart Parsing with Feature Based Grammars

Here is our general algorithm for active chart parsing.

1. Make initial chart and agenda.

2. Repeat until agenda is empty:

   1. Take first arc from agenda.

   2. Add arc to chart. (Only do this if edge is not already on the chart!)

   3. Use the fundametal rule to combine this arc with arcs from the chart. Any edges obtained in this way should be added to the agenda.

   4. Make hypotheses (i.e., active edges) about new constituents based on the arc and the rules of the grammar. Add these new arcs to the agenda.

   End repeat

3. See if the chart contains a passive edge from the first node to the last node that has the label s. If "yes", succeed. If "xno", fail.

The general procedure can stay completely unchanged. We only have to take care in those places where we deal with categories. Let's go through an example and see where we have to adapt the general algorithm for dealing with feature based grammars.

Assume we want to parse the sentence mia dances with the grammar given above. We will use the general algorithm in a bottom-up fashion.

Step 1. We initialize the chart and agenda:

Step 2a. We take the first arc from the agenda.

Step 2b. Now, what do we have to check before we add the arc to the chart? When working with plain context free grammars this was simple: we just checked whether there already was an arc in the chart that was identical to the one we wanted to add. Instead of doing that we will now check whether there is an arc that starts and ends in the same position, has the dot in the same position, and the feature structures in the rule subsume all corresponding feature structures in the new arc.

If we, e.g., had the arc

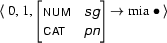
in the chart, we would clearly not want add our new arc. The two arcs are not identical but they contain exactly the same information. And, therefore, our condition for when to not add is satisfied: all feature structures of the arc in the chart subsume all corresponding feature structures in the new arc. In particular,

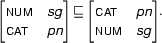
What if we had the arc

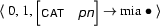
in the chart? All feature structures in this arc subsume the corresponding feature structures in the new arc. So, we wouldn't add the new arc in this case. Let's think a bit about this. Why does it make sense? The arc that's already in the chart is more general than the new one. This means that all combinations that we might be able to do with the new arc can also be done with the one that's already in the chart, as everything that's unifiable with

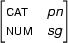
is also unifiable with

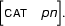
So, adding the new arc to the chart would not allow us to do any more combinations than we can already do. Hence, we don't need it in the chart.

Returning to the example, we add the new arc to the chart.

Step 2c. We try to apply the fundamental rule. Nothing happens as there are not yet any active arcs in the chart that we could combine with the new one.

Step 2d. The arc we are looking at is passive and we are doing bottom-up parsing, so we have to build new hypotheses in this step. When dealing with plain context free grammars we were looking for grammar rules such that the first category on the right hand side was identical to the category provided by the passive arc. Now, when dealing with feature based grammars, we are going to look for grammar rules such that the first category on the right hand side is unifiable with the category provided by the passive arc. So, in our example we are going to look for all grammar rules such that the first symbol in the right hand side is unifiable with

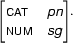
The rule

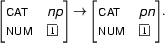
is such a rule. The new arc is build from this rule after carrying out the unification. It looks like this: