13.3 Comparing Feature Structures: Subsumption
We said above that feature structures are essentially sets of properties. Given two different sets of properties an obvious thing to do is to compare the information they contain. A particularly important concept for comparing two feature structures is subsumption.
A feature structure 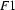 subsumes (
subsumes (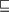 ) another feature structure
) another feature structure 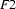 , iff all the information that is contained in
, iff all the information that is contained in 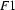 is also contained in
is also contained in 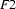 .
.
The following two feature structures for instance subsume each other.

The both contain exactly the same information, since the order in which the features are listed in the matrix is not important.
And how about the following two feature structures?

Well, the first one subsumes the second, but not vice versa. Every piece of information that is contained in the first feature structure is also contained in the second, but the second feature structure contains additional information.
A final example: Do the following feature structures subsume each other?

The first one doesn't subsume the second, because it contains information that the second doesn't contain, namely 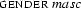 . But, the second one doesn't subsume the first one either, as it contains
. But, the second one doesn't subsume the first one either, as it contains 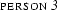 which is not part of the first feature structure.
which is not part of the first feature structure.
Notice that the subsumption relation between feature structures is somewhat similar to the subset relation between sets: Feature structure 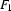 subsumes features structure
subsumes features structure 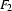 iff all the information of
iff all the information of 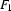 is also in
is also in 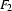 . Set
. Set  is a subset of set
is a subset of set 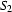 iff all elements of
iff all elements of  are also elements of
are also elements of 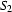 .
.