1.5 Finite State Methods in Computational Linguistics and their Limitations

We have seen in this chapter that finite state machines are very simple. As a consequence, there are limitations to what they can do. It is, for example, not possible to write an FSM that generates the language 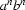, i.e. the set of all strings which consist of a (possibly empty) block of as followed by a (possibly empty) block of bs of exactly the same length). That is, viewed mathematically, FSAs have certain expressive weaknesses. This also limits their expressive adequacy from a linguistic point of view, because many linguistic phenomena can only be described by languages which cannot be generated by FSAs. In fact, even the language 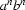is linguistically relevant, since many linguistic constructions require `balanced' structures.

However, there are linguistic applications where the expressive power of finite state methods seems to be sufficient and FSAs have been used and are used a lot for all kinds of tasks in computational linguistics; the flip side of their expressive weakness being that they usually behave very well computationally. If you can find a solution based on finite state methods, your implementation will probably be efficient.

Areas where finite state methods have been shown to be particularly useful are phonological and morphological processing. We will see some simple examples for that in the next chapter. But finite state methods have also been applied to syntactic analysis. Although they are not expressive enough if a full syntactic analysis is required there are many applications where a partial syntacic analysis of the input is sufficient. And such partial analyses can be constructed with cascades of finite state automata (or rather transducers, which we will learn about in the next chapter) where one machine is applied to the output of another. Furthermore, hidden markov models, which are very common for speech recognition and part of speech tagging, can be seen as a variant of FSAs which assigns probabiltites to its transitions.