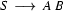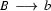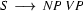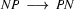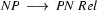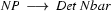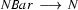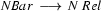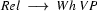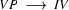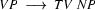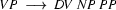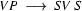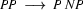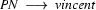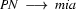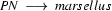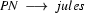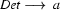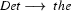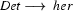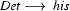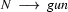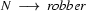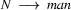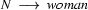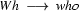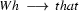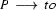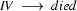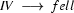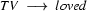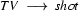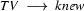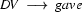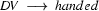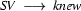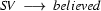7.1 Context Free Grammars

Let's begin by going through some basic ideas about context-free grammars. I'll start by using simple grammars that generate formal languages, rather than natural language examples, as the formal examples are typically shorter.

7.1.1 The Basics

Here's a simple context free grammar (CFG):

$S\ \longrightarrow\ A\ B$

$S\ \longrightarrow\ A\ S\ B$

$A\ \longrightarrow\ a$

$B\ \longrightarrow\ b$

Some terminology. The 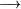$\longrightarrow$ is called the rewrite arrow, and the four expressions listed above are called context free rules (you may also see them called rewrite rules, or something similar).

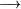Apart from the $\longrightarrow$ , there are two sorts of symbols in this grammar: terminal symbols and non-terminal symbols. In the above grammar, the terminal symbols are `a' and `b', and the non-terminal symbols are `S', `A', and `B'. Terminal symbols never occur to the left of a rewrite arrow. Non-terminal symbols may occur either to the right or the left of the rewrite arrow (for example, the `S' in the above grammar occurs both to the right and the left of $\longrightarrow$ in the second rule). Every context free grammar has one special symbol, the start or sentence symbol, which is usually written `S'. Some context free grammars also use another special symbol, namely $\epsilon$ , for the empty string. The $\epsilon$ symbol can only occur on the right hand side of context free rules. 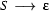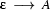For example, we could add the rule $S\ \longrightarrow\ \epsilon$ to the above grammar, but we could not add $\epsilon\ \longrightarrow\ A$ .

The simplest interpretation of context free grammars is the rewrite interpretation. This views CFGs as rules which let us rewrite the start symbol S to other strings: each rule is interpreted as saying that we can replace an occurrence of the symbol on the left side of the rule by the symbol(s) on the right side.

For example, the above grammar lets us rewrite `S' to `aabb':

S
ASB	Rule 2
aSB	Rule 3
aSb	Rule 4
aABb	Rule 1
aaBb	Rule 3
aabb	Rule 4

Such a sequence is called a derivation of the symbols in the last row. For example, the above sequence is a derivation of the string `aabb'. Note that there may be many derivations of the same string. For example,

S
ASB	Rule 2
ASb	Rule 4
aSb	Rule 3
aABb	Rule 1
aAbb	Rule 4
aabb	Rule 3

is another derivation of `aabb'.

Why are such grammars called `context free'? Because all rules contain only one symbol on the left hand side --- and wherever we see that symbol while doing a derivation, we are free to replace it with the stuff on the right hand side. That is, the `context' in which a symbol on the left hand side of a rule occurs is unimportant --- we can always use the rule to make the rewrite while doing a derivation. (There are more complex kinds of grammars, with more than one symbol on the left hand side of the rewrite arrow, in which the symbols to the right and left have to be taken into account before making a rewrite. Such grammars can be linguistically important, but we won't study them in this course.)

The language generated by a context free grammar is the set of terminal symbols that can be derived starting from the start symbol `S'. For example, the above grammar generates the language 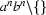$a^n b^n \backslash \{\}$ (the language consisting of all strings consisting of a block of as followed by a block of bs of equal length, except the empty string). And if we added the rule 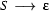$S\ \longrightarrow\ \epsilon$ to this grammar we would generate the language a^n b^n .

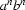A language is called context free if it is generated by some context free grammar. For example, the language 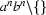$a^n b^n \backslash \{\}$ is context free, and so is the language 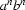a^n b^n , for we have just seen that these can be produced by CFGs. Not all languages are context free. For example, 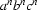a^n b^n c^n is not. That is, no matter how hard you try to find CFG rules that generate this language, you won't succeed. No CFG can do the job.

7.1.2 The Tree Admissibility Interpretation

While the rewrite interpretation of CFGs is important, there is a more fundamental way of thinking about CFGs, namely as tree admissibility rules.

A parse tree is a finite tree all of whose interior nodes (that is, nodes with daughters) are licensed or admitted by a grammar rule. What does this mean? Let's look at an example:

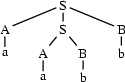
This tree is licensed by our grammar --- that is, the presence of every node with daughters can be justified by some rule. For example. the top node is ok, because under the tree admissibility interpretation we read 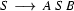$S\ \longrightarrow\ A\ S\ B$ as saying: A tree node labelled 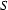can have exactly three daughters, labelled (reading left to right) , , 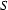and . The node labelled A is ok, because under the tree admissibility we read the rule 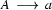$A\ \longrightarrow\ a$ as saying: A tree node labelled can have exactly one daughter which is labelled . Similarly, all the other nodes with daughters are `justified' or `admitted' by other rules (the terminal nodes of the tree don't need to be justified).

If you think about it, you will see there is a close correspondence between parse trees and derivations: every derivation corresponds to a parse tree, and every parse tree corresponds to (maybe many) derivations. For example, the tree above corresponds to both our earlier derivations of `aabb'.

The tree admissibility interpretation is important for two reasons. First, it is the linguistically most fundamental interpretation. We don't think of natural language as a bunch of strings that need rewriting --- we think of natural language sentences, and noun phrases and so on as having structure, tree structure. Thus we think of CFG rules as telling us which tree structures we have.

Second, the idea of parse trees brings us to an important concept: ambiguity. A string is ambiguous if it has two distinct parse trees. Note: I said `parse trees', not `derivations'. For example, we derived the string `aabb' in two different ways from our little grammar --- but both ways correspond to the same derivation tree. That is, the string `aabb' is not ambiguous in this grammar. And in fact, no string this grammar generates is ambiguous.

But some grammars do generate ambiguous strings. One of this week's exercises is to come up with a simple example of such a grammar.

7.1.3 A Little Grammar of English

The above ideas adapt straightforwardly to natural languages. But with natural languages it is useful to draw a distinction between rules which have syntactic categories on the right hand side, and rules which have only words on the right hand side (these are called lexical rules).

Here's a simple grammar of English. First we have the following rules:

$S \ \longrightarrow\ NP\ VP$

$NP \ \longrightarrow\ PN$

$NP \ \longrightarrow\ PN\ Rel$

$NP \ \longrightarrow\ Det\ Nbar$

$NBar\ \longrightarrow\ N$

$NBar\ \longrightarrow\ N\ Rel$

$Rel \ \longrightarrow\ Wh\ VP$

$VP \ \longrightarrow\ IV$

$VP \ \longrightarrow\ TV\ NP$

$VP \ \longrightarrow\ DV\ NP\ PP$

$VP \ \longrightarrow\ SV\ S$

$PP \ \longrightarrow\ P\ NP$

Then we have the following lexical rules.

$PN\ \longrightarrow\ vincent$

$PN\ \longrightarrow\ mia$

$PN\ \longrightarrow\ marsellus$

$PN\ \longrightarrow\ jules$

$Det\longrightarrow\ a$

$Det\longrightarrow\ the$

$Det\longrightarrow\ her$

$Det\longrightarrow\ his$

$N \ \longrightarrow\ gun$

$N \ \longrightarrow\ robber$

$N \ \longrightarrow\ man$

$N \ \longrightarrow\ woman$

$Wh\ \longrightarrow\ who$

$Wh\ \longrightarrow\ that$

$P \ \longrightarrow\ to$

$IV\ \longrightarrow\ died$

$IV\ \longrightarrow\ fell$

$TV\ \longrightarrow\ loved$

$TV\ \longrightarrow\ shot$

$TV\ \longrightarrow\ knew$

$DV\ \longrightarrow\ gave$

$DV\ \longrightarrow\ handed$

$SV\ \longrightarrow\ knew$

$SV\ \longrightarrow\ believed$

So in this grammar, our terminal symbols are the words. There is a special word for the symbols (such as N, PN, and Det) which occur in lexical rules: they are called preterminal symbols.

This grammar is unambiguous. That is no string has two distinct parse trees. (Incidentally, this means that it is not a realistic grammar of English: all natural languages are highly ambiguous.) But it does display an interesting (and troublesome) phenomenon called local ambiguity.

Consider the sentence ``The robber knew Vincent shot Marsellus''. This has a unique parse tree in this grammar. But now look at the first part of it: ``The robber knew Vincent''. This is also a sentence according to this grammar --- but not when considered as a part of ``The robber knew Vincent shot Marsellus''. This can be a problem for a parser. Locally we have something that looks like a sentence --- and a parser may prove that this part really is a sentence according to the grammar. But this information does not play a role in analyzing the larger sentence of which it is a part.