2.1.1 Finite State Parsers

So, in the case of a finite state parser the parser output should tell us about the transitions that had to be made in the FSA when the input was recognized. That is, the output should be a sequence of nodes and arcs. If we, for example, gave the input [h,a,h,a,!] to a parser for our first laughing automaton, it should give us [1,h,2,a,3,h,2,a,3,!,4].

There is a fairly standard technique in Prolog for turning a recognizer into a parser: add one or more extra arguments to keep track of the structure that was found. We will now use this technique to turn recognize1/2 of the last chapter into parse1/3, i.e. a parser for FSAs without jump arcs.

In the base clause, when the input is read and the FSA is in a final state, all we have to do is record that final state. So, we turn

recognize1(Node,[]) :-
    final(Node).

into

parse1(Node,[],[Node]) :-
    final(Node).

Then let's look at the recursive clause. The recursive clause of recognize1/2 looked as follows:

recognize1(Node1,String) :-
    arc(Node1,Node2,Label),
    traverse1(Label,String,NewString),
    recognize1(Node2,NewString).

And here is the recursive clause of parse/1:

parse1(Node1,String,[Node1,Label|Path]) :-
    arc(Node1,Node2,Label),
    traverse1(Label,String,NewString),
    parse1(Node2,NewString,Path).

The parser records the state the FSA is in and the symbol it is reading on the transition it is taking from this state. The rest of the path, i.e. the sequence of states and arcs that the FSA will take from Node2 onwards, will be specified in the recursive call of parse1 and collected in the variable Path.

The only thing that's left to do, is to adapt the driver predicates test1/1 and generate1/1. The new driver predicates look as follows:

testparse1(Symbols,Parse) :-
    initial(Node),
    parse1(Node,Symbols,Parse).

genparse1(Symbols,Parse) :-
    testparse1(Symbols,Parse).

Now, let's step through an example to have a look at how the output is being built in the extra argument during recognition. Assume that we have loaded the Prolog representation of our first laughing automaton in to the Prolog database. So the database contains the following facts:

initial(1).
final(4).
arc(1,2,h).
arc(2,3,a).
arc(3,4,!).
arc(3,2,h).

We ask Prolog the following query:

?- testparse1([h,a,!],Parse).

Prolog retrieves 1 as the only initial node in this FSA and calls parse1/1 instantiated as

parse1(1,[h,a,!],Parse).

Next, Prolog has to retrieve arcs starting in node 1 from the database. It finds arc(1,2,h), which it can use because the first symbol in the input is h as well. So, Parse is unified with [1,h|_G67] where _G67 is some Prolog internal variable. Prolog then makes a recursive call (the first recursive call) of parse1 with

parse1(2,[a,!],_G67).

Now, Prolog finds arc(2,3,a) in the database. So, _G67 gets unified with [2,a|_G68] (_G68 again being some internal variable) and Prolog makes the second recursive call of parse1:

parse1(3,[!],_G68).

Using arc(3,4,!) the last symbol of the input can be read and _G68 gets instantiated to [3,!|_G69]. The next recursive call of parse1 (parse1(4,[],_G69)) matches the base clause. Here, _G69 gets instantiated to [4], instantiating _G68 to [3,!,4], _G67 to [2,a,3,!,4], and Parse to [1,h,2,a,3,!,4] as Prolog comes back out of the recursion. If you have trouble understanding how the output gets assembled, draw a search tree for the query parse1(1,[h,a,!],Parse). Note, how with every recursive call of parse1 the third argument gets instantiated with a list. The first two elements of this list are the state the FSA is currently in and the next symbol it reads; the rest of the list is an uninstantiated variable at first, but gets further instantiated by the next recursive call of parse1.

2.1.2 Separating out the Lexicon

In the practical session of the last chapter you were asked to construct a finite state automaton recognizing those English noun phrases that can be built from the words the, a, wizard, witch, broomstick, hermione, harry, ron, with, fast. The FSA that you came up with probably looked similar to this:

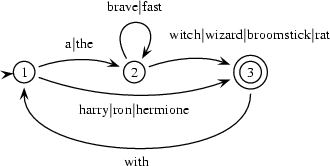
which is

  
initial(1).
final(3).
arc(1,2,a).
arc(1,2,the).
arc(2,2,brave).
arc(2,2,fast).
arc(2,3,witch).
arc(2,3,wizard).
arc(2,3,broomstick).
arc(2,3,rat).
arc(1,3,harry).
arc(1,3,ron).
arc(1,3,hermione).
arc(3,1,with).

in Prolog.

Now, what would Prolog answer, if we used the parser of the previous section on this automaton to parse the input [the,fast,wizard]? It would return [1,the,2,fast,2,wizard,3]. This tells us how the FSA was traversed for recognizing that this input is indeed a noun phrase. But in a way, it would be even nicer, if we got a more abstract explanation saying, e.g., that [the,fast,wizard] is a noun phrase because it consists of a determiner followed by an adjective which is followed by a common noun. That is, we would like the parser to return something like this:

[1,det,2,adj,2,noun,3].

Actually, you were probably already making a similar abstraction when you were thinking about how to construct that FSA. You were probably thinking: ``Well, a noun phrase starts with a determiner, can be followed by zero or more adjectives, and ends in a noun; the and a are the determiners that I have, so I need a the and an a transition from state 1 to state 2.'' And, in fact, it would be a lot nicer, if you could specify transitions in the FSA based on categories like determiner, common noun, and so on and additionally give a separate lexicon which specifies what words belong to a category. Like this, for example:

initial(1).           lex(a,det).
final(3).             lex(the,det).
arc(1,2,det).         lex(fast,adj).
arc(2,2,adj).         lex(brave,adj).
arc(2,3,cn).          lex(witch,cn).
arc(1,3,pn).          lex(wizard,cn).
arc(3,1,prep).        lex(broomstick,cn).
                      lex(rat,cn).
                      lex(harry,pn).
                      lex(hermione,pn).
                      lex(ron,pn).
                      lex(with,prep).

It's not very difficult to change our recognizer to work with FSA specifications that, like the above, define their transitions in terms of categories instead of symbols and then use a lexicon to map those categories to symbols or the other way round. The only thing that changes is the definition of the traverse predicate. We don't simply compare the label of the arc with the next symbol of the input anymore, but have to access the lexicon to check whether the next symbol of the input is a word of the category specified by the label of the arc. That means, instead of

traverse2('#',String,String).
traverse2(Label,[Label|Symbols],Symbols).

we use

traverse3('#',String,String).
traverse3(Label,[Symbol|Symbols],Symbols) :-
   lex(Symbol,Label).